Quantum computer scales up by mitigating errorsbb
The idea that quantum computers might one day solve complex problems at lightning speed on microscopic chips has long been touted. But the race to show that these processors can outperform their classical counterparts is a difficult one, in which every success is cause for celebration. Writing in Nature, Kim et al.1 report a quantum-computational feat that is well beyond the capability of classical simulation: the determination, using 127 quantum bits (qubits), of the magnetization of a model quantum material. The system’s fundamental advantage pertains to scale rather than speed: no classical computer has enough memory to encode the possibilities computed by the 127 qubits.
有人早就宣称,量子计算机有朝一日可以在微小芯片上以闪电般的速度解决复杂问题。但是,证明这些处理器能够胜过它们的经典对应物的竞赛是一场艰苦的战斗,每一次成功都值得庆祝。Kim等人在《自然》杂志上发表文章[1],报告了一项量子计算壮举,这项壮举远远超出了经典模拟的能力范围:使用127个量子位(qubit),确定了一个模型量子材料的磁化。该系统的根本优势在于规模而非速度:没有经典计算机有足够的内存来编码127个qubits计算的可能性。
"Pertains" means to relate or belong to a particular subject or topic. It can be used in both spoken and written English, and is a formal way of expressing that something is relevant or connected to a certain matter.
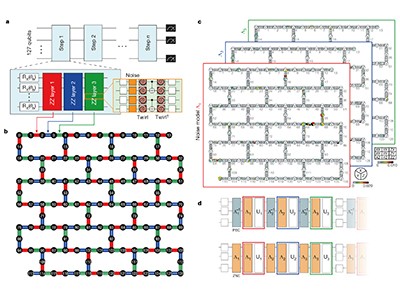
A quantum computer that can outperform a classical computer is said to display quantum advantage, but this is an elusive concept with many facets. It was once synonymous with the idea that a quantum processor could accelerate computation exponentially, by using the fact that qubits can encode a superposition of entire memories containing the 1s and 0s that store information in conventional computers. Over time, it has come to refer to more-modest quantum speed-ups in the computing times of algorithms used in chemistry, materials and logistics research2.
据说,能够胜过经典计算机的量子计算机展示了量子优势,但这是一个具有许多方面的难以捉摸的概念。曾经,它与量子处理器能够通过使用量子比特可以编码包含在传统计算机中存储信息的1和0的整个存储器的叠加来指数级加速计算的想法同义。随着时间的推移,它已经转向更为温和的量子加速,在化学、材料和物流研究中使用的算法的计算时间上的加速。
Developing the full potential of quantum computers requires devices that can correct their own errors. Such errors occur all too frequently, and correcting them is a difficult task needing a large, multidisciplinary engineering effort. The resulting systems, known as fault-tolerant quantum computers, will consist of thousands of high-quality qubits, held in check by an exquisite control system. But is it possible to achieve useful quantum advantage in the interim, before accomplishing full fault tolerance?
发掘量子计算机的全部潜能需要能够纠正自身错误的设备。这些错误经常发生,纠正它们需要大量跨学科的工程努力。最终的系统,称为容错量子计算机,将由数千个高质量的量子比特组成,并由一个精美的控制系统控制。但在实现完全的容错之前,在过渡期间是否有可能实现有用的量子优势呢?
It has been conjectured that some meaningful problems can be solved without quantum error correction, using an approach called noisy intermediate-scale quantum computation2. This technique encodes the problem in qubits that need not be perfect, in a state that requires relatively few qubits, and these are then measured quickly, before an error can corrupt the computation. However, algorithms for solving useful problems require that, to reach sufficient accuracy, thousands of low-error operations be completed before measurement. In the end, this might not be possible without fault tolerance through quantum error correction.
有人猜想,使用一种称为嘈杂中等规模量子计算(noisy intermediate-scale quantum computation)的方法可以解决一些有意义的问题,而不需要量子纠错(quantum error correction)2。这种技术将问题编码到不需要完美的量子比特(qubits)中,并且需要相对较少的量子比特,然后快速地进行测量,以免出现误差。然而,解决有用问题的算法需要在测量之前完成数千次低误差操作,以达到足够的精度。最终,如果没有通过量子纠错实现容错,这可能是不可能的。
In 2019, a programmable superconducting quantum computer was reported to have outperformed the most powerful conventional computers34. But the processor was benchmarked with a task designed solely for this purpose — sampling the output of a random circuit containing quantum logic gates. Instead, Kim et al. sought to simulate the dynamics of a system that is perhaps more appealing to physicists: a two-dimensional Ising model, which is now used across many areas of physics, but was originally devised to describe magnetic materials. The approach is in the spirit of US physicist Richard Feynman’s idea of simulating one quantum system (the Ising model) by using another (the quantum computer)5.
在2019年,据报道,一台可编程的超导量子计算机已经超越了最强大的传统计算机3,4。但是,该处理器的基准测试任务是专门为此设计的——采样包含量子逻辑门的随机电路的输出。相反,金等人试图模拟一个对物理学家可能更有吸引力的系统的动力学:一个二维伊辛模型,现在在许多物理领域都得到了应用,但最初是为了描述磁性材料而设计的。这种方法符合美国物理学家理查德·费曼使用一个量子系统(伊辛模型)来模拟另一个量子系统(量子计算机)的思想5。
The Ising model conceives of the ‘spins’ (intrinsic angular momenta) of electrons in a magnetic material as discrete variables: each spin can point in any direction, but a measurement will cast it as either up or down. These spins are arranged on a lattice and, when subjected to an external magnetic field, they align, resulting in the collective magnetization of the material. Kim and colleagues’ goal was to accurately measure the average magnetization for selected clusters of spins — rather than the more challenging problem of determining the exact state of the entire system.
The authors modelled the way that the system changes in time as a sequence of operations on qubits and pairs of qubits, configured as 2,880 two-qubit gates. Their quantum hardware and control system were both state-of-the-art devices, but estimating the average magnetization still required advanced techniques to mitigate any errors67. Quantum error mitigation is a post-processing method that uses software to compensate for the noise generated during a calculation, and should not be confused with quantum error correction. The idea is that a quantum computation that uses a ‘small’ number of qubits (up to 68) can be verified with brute-force classical simulation, lending credibility to the idea that errors are similarly mitigated for larger systems that cannot be verified classically.
Kim et al. verified their error-mitigation scheme by computing the magnetization of a single spin in a simulation involving all 127 qubits. Before mitigating the errors, the authors’ results were strongly affected by noise, but their post-processing technique restored the correct magnetization (Fig. 1). They also compared their calculation with approximate results from two classical-simulation techniques. Both methods are known to break down when the external magnetic field is oriented in a direction between those perpendicular and parallel to the spins, a situation in which the quantum nature of the system is particularly important.
Ising模型将磁性材料中电子的“自旋”(内禀角动量)构想为离散变量:每个自旋可以指向任何方向,但测量会将其投射为向上或向下。这些自旋排列在晶格上,当受到外部磁场的作用时,它们会排列成一列,导致材料的集体磁化。Kim等人的目标是准确测量所选自旋簇的平均磁化度-而不是确定整个系统的确切状态的更具挑战性的问题。
作者将系统随时间变化的方式建模为qubit和qubit对的一系列操作,配置为2,880个双量子比特门。他们的量子硬件和控制系统都是最先进的设备,但估计平均磁化仍需要先进的技术来减轻任何错误[6],[7]。量子误差减轻是一种后处理方法,它使用软件来补偿计算期间生成的噪声,不应与量子误差纠正混淆。这个想法是,一个使用“小”量子比特数(最多68个)的量子计算可以通过蛮力经典模拟进行验证,从而使人相信对于无法经典验证的更大系统同样减轻了错误。
Kim等人通过计算涉及所有127个量子比特的模拟中单个自旋的磁化来验证他们的误差减轻方案。在减轻错误之前,作者的结果受到噪声的强烈影响,但他们的后处理技术恢复了正确的磁化(图1)。他们还将计算结果与两种经典模拟技术的近似结果进行了比较。当外部磁场定向于垂直于自旋和平行于自旋之间的方向时,这两种方法都会崩溃,这种情况下系统的量子性质特别重要。
Figure 1 | Mitigating errors in quantum computation. a, Kim et al.1 used a quantum computer to simulate the spin (intrinsic angular momentum) of electrons in a model quantum material. The spins are arranged on a lattice, point up or down when measured, and align in the presence of an external magnetic field, causing the material to magnetize. b, The authors computed the magnetization of a single spin corresponding to one quantum bit (qubit) in a simulation involving 127 qubits, and used a post-processing method to mitigate quantum errors. They compared their calculation with approximate results from two classical-simulation techniques, known as MPS and isoTNS, both of which are inaccurate when the magnetic field is oriented in a direction between those perpendicular and parallel to the spins. (Adapted from Fig. 4b of ref. 1.)
图1 | 量子计算中的误差缓解。 a,Kim等人[1]利用量子计算机模拟了模型量子材料中电子的自旋(内禀角动量)。这些自旋排列在晶格上,当测量时向上或向下,且在外部磁场的作用下排列一致,导致材料磁化。b,作者计算了127个量子比特(qubit)模拟中一个单个自旋的磁化,并使用后处理方法缓解了量子误差。他们将计算结果与两种经典模拟技术(MPS和isoTNS)的近似结果进行了比较,这两种技术在磁场方向介于自旋垂直和平行之间时都不准确。(改编自参考文献1的图4b。)
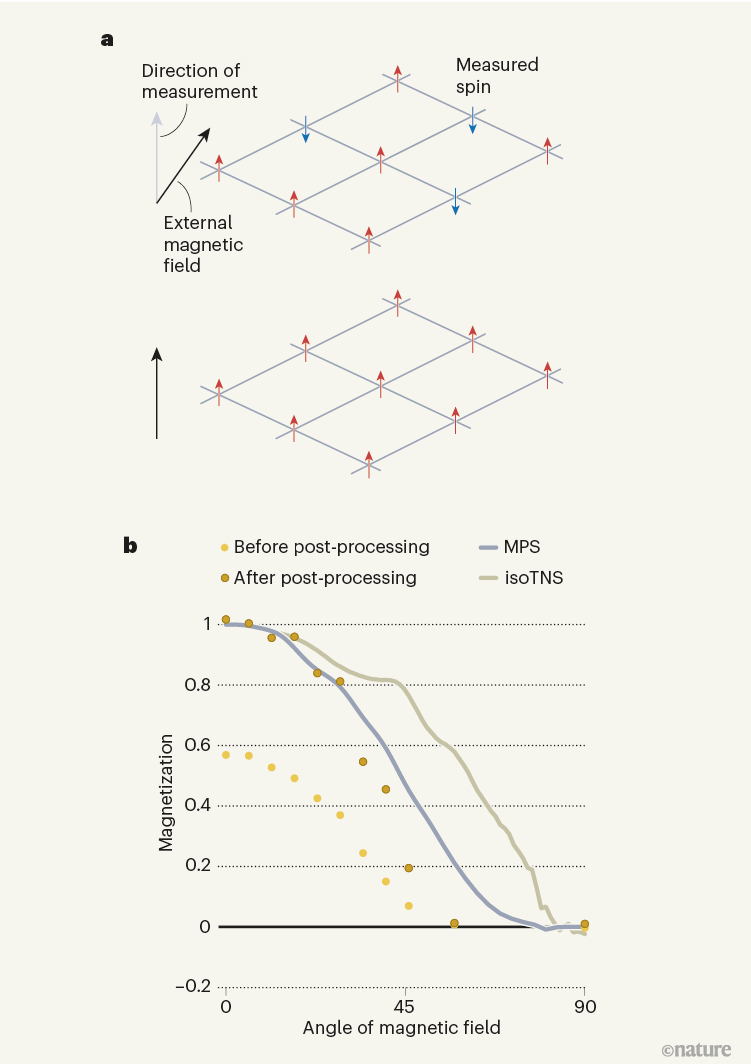
The quantum-computational advantage that Kim et al. demonstrated is one of scale. In implementing a quantum processor with 127 qubits, the authors showed that a quantum computer could go beyond a previous experiment with 27 qubits8 and thereby decisively exceed the limits set by classical methods. In terms of the computational time, the quantum speed-up reported was very modest — only two to three times faster than a classical simulation method called isoTNS, which produces inaccurate results (see Fig. 1b).
So does this advance improve the prospects for applying quantum computation to industrially relevant problems? The answer is most probably no: such algorithms must involve a much larger number of qubits and many more consecutive gate operations to be competitive with high-performance classical supercomputers, and these quantum computations would inevitably drown in noise arising from qubit errors.
Instead, Kim and co-workers’ results herald further opportunities for quantum processors to emulate physical systems that are far beyond the reach of conventional computers. As quantum hardware improves, processors will be capable of longer computations than those currently possible, and such computations will require advanced post-processing and quantum error-mitigation methods that can handle large data sets9. Techniques such as Kim and colleagues’ error-mitigation method will drive the development of device technology, control systems and software by providing applications that could offer useful quantum advantage beyond quantum-computing research — and will pave the way for truly fault-tolerant quantum computing.
金*等人展示了量子计算的规模优势。通过实现一个拥有127个量子比特的量子处理器,作者展示了量子计算机可以超越之前27个量子比特实验[8],从而决定性地超出了经典方法所设定的极限。就计算时间而言,量子加速报告的速度非常适中,只比一个称为isoTNS的产生不准确结果的经典模拟方法快两到三倍,(见图1b)。
那么,这一进展能否改善量子计算在工业相关问题中的应用前景?答案很可能是否定的:这样的算法必须涉及更多的量子比特和更多的连续门操作,才能与高性能经典超级计算机竞争,这些量子计算不可避免地会淹没在由量子比特误差引起的噪声中。
相反,金和他的同事的研究结果预示着量子处理器进一步模拟远远超出传统计算机的物理系统的机会。随着量子硬件的改进,处理器将能够进行比目前可能更长的计算,这些计算将需要处理大数据集的先进后处理和量子误差缓解方法[9]。像金和同事的误差缓解方法这样的技术将通过提供超越量子计算研究的有用量子优势的应用,推动设备技术、控制系统和软件的发展,并为真正容错的量子计算铺平道路。
总结:
The article provides an overview of recent progress in the field of quantum computing, highlighting a report published in Nature by Kim et al. which describes the use of a quantum computer to determine the magnetization of a model quantum material. In their experiment, the authors used 127 qubits to simulate the dynamics of a two-dimensional Ising model and measure the average magnetization for selected clusters of spins. The Ising model is a way to conceive of the intrinsic angular momenta of electrons in a magnetic material as discrete variables, which are arranged on a lattice and align in the presence of an external magnetic field, resulting in the material's magnetization.
The article notes that the system's advantage pertains to scale, rather than speed, as no classical computer has enough memory to encode the possibilities computed by the 127 qubits. However, the article also discusses the challenges of achieving useful quantum advantage, as algorithms must involve a much larger number of qubits and many more consecutive gate operations to be competitive with high-performance classical supercomputers. Additionally, quantum computations would inevitably generate noise arising from qubit errors, which would need to be mitigated through advanced post-processing and quantum error-mitigation methods.
The article also describes the authors' error-mitigation scheme, which involved using software to compensate for noise generated during the calculation. The authors verified their scheme by computing the magnetization of a single spin in a simulation involving all 127 qubits. Before mitigating the errors, the results were strongly affected by noise, but their post-processing technique restored the correct magnetization. The article notes that techniques such as the error-mitigation method developed by Kim and colleagues will drive the development of device technology, control systems, and software by providing applications that could offer useful quantum advantage beyond quantum-computing research, paving the way for truly fault-tolerant quantum computing.
In conclusion, while the report by Kim et al. represents an important milestone in the field of quantum computing, the article highlights the challenges that remain in achieving useful quantum advantage and developing fault-tolerant quantum computers. However, the article also notes that the results of the experiment provide further opportunities for quantum processors to emulate physical systems that are far beyond the reach of conventional computers, as quantum hardware improves and processors become capable of longer computations.
本文概述了量子计算领域的最新进展,重点介绍了Kim等人在自然界上发表的一篇报告,该报告描述了使用量子计算机来确定模型量子材料的磁化。在他们的实验中,作者使用127个量子比特来模拟二维伊辛模型的动力学,并测量所选自旋簇的平均磁化。伊辛模型是将磁性材料中电子的固有角动量构思为离散变量的一种方式,这些变量排列在晶格上,并在外部磁场的作用下排列,从而形成材料的磁化。
文章指出,该系统的优势在于规模,而不是速度,因为没有经典计算机具有足够的内存来编码由127个量子比特计算出的可能性。然而,文章还讨论了实现有用的量子优势的挑战,因为算法必须涉及更多的量子比特和更多的连续门操作,才能与高性能的经典超级计算机竞争。此外,量子计算不可避免地会产生由量子比特错误引起的噪声,需要通过先进的后处理和量子误差缓解方法来减轻。
文章还描述了作者的误差缓解方案,其中使用软件来补偿计算期间产生的噪声。作者通过计算涉及所有127个量子比特的模拟中的单个自旋的磁化来验证他们的方案。在减轻误差之前,结果受到噪声的强烈影响,但是他们的后处理技术恢复了正确的磁化。文章指出,像Kim和同事开发的误差缓解方法这样的技术将通过提供超越量子计算研究的有用量子优势应用程序来推动设备技术、控制系统和软件的发展,为真正的容错量子计算铺平道路。
总之,虽然Kim等人的报告代表了量子计算领域的重要里程碑,但文章强调了实现有用的量子优势和开发容错量子计算机所面临的挑战。然而,文章还指出,实验结果为量子处理器模拟远远超出传统计算机范围的物理系统提供了进一步的机会,随着量子硬件的改进和处理器变得能够进行更长时间的计算。
原文摘要:
Quantum computing promises to offer substantial speed-ups over its classical counterpart for certain problems. However, the greatest impediment to realizing its full potential is noise that is inherent to these systems. The widely accepted solution to this challenge is the implementation of fault-tolerant quantum circuits, which is out of reach for current processors. Here we report experiments on a noisy 127-qubit processor and demonstrate the measurement of accurate expectation values for circuit volumes at a scale beyond brute-force classical computation. We argue that this represents evidence for the utility of quantum computing in a pre-fault-tolerant era. These experimental results are enabled by advances in the coherence and calibration of a superconducting processor at this scale and the ability to characterize1 and controllably manipulate noise across such a large device. We establish the accuracy of the measured expectation values by comparing them with the output of exactly verifiable circuits. In the regime of strong entanglement, the quantum computer provides correct results for which leading classical approximations such as pure-statebased 1D (matrix product states, MPS) and 2D (isometric tensor network states, isoTNS) tensor network methods2,3 break down. These experiments demonstrate a foundational tool for the realization of near-term quantum applications4,5.
量子计算承诺在某些问题上比其经典对应物提供大幅加速。然而,实现其全部潜力的最大障碍是这些系统固有的噪音。这个挑战的广泛接受的解决方案是实现容错量子电路,这对于当前的处理器来说是不可达的。在这里,我们报告了对一个有噪音的127量子比特处理器的实验,并展示了在超出暴力经典计算规模的电路体积上测量准确期望值的能力。我们认为这代表了在容错前的量子计算时代中,量子计算的实用性证据。这些实验结果得益于在这个规模的超导处理器中相干性和校准的进展以及在这样一个大型设备上表征和可控操纵噪音的能力。我们通过将其与确切可验证电路的输出进行比较,建立了测量期望值的准确性。在强纠缠的区域,量子计算机提供了正确的结果,而主要的经典近似,如基于纯态的1D(矩阵乘积状态,MPS)和2D(等距张量网络状态,isoTNS)张量网络方法2、3则失败了。这些实验证明了实现近期量子应用4,5的基础工具。
Due to limited number of qubits in the NISQ era, all logical qubits in the quantum circuit are directly implemented by physical qubits without QEC.
由于NISQ时代量子比特数量有限,量子电路中的所有逻辑比特都是直接由物理比特实现的,没有使用QEC。
qubit mapping problem
Definition: Given an input quantum circuit and the coupling graph of a quantum device, find an initial mapping and the intermediate qubit mapping transition (by inserting SWAPs) to satisfy all two-qubit constraints and try to minimize the number of additional gates and circuit depth in the final hardware-compliant circuit.
定义:给定一个输入的量子电路和一个量子设备的耦合图,找到一个初始映射和中间的量子比特映射转换(通过插入SWAP),以满足所有的两比特约束,并尽可能地减少额外门的数量和电路深度,得到最终的符合硬件要求的电路。
Intuitively, I feel that the error in global optimization problems can be alleviated.
Advantages and Disadvantages
We can avoid performing some redundant operations during quantum computation.
We can obtain the quantum operation sequences we want. However, the problem lies in the inability to perform real-time decoding and error correction to achieve timely recovery of errors. The latest progress is to use FPGA and ASIC chips for hardware decoding, achieving feedback within 1 microsecond delay.
- Giscus
Last update: 2023-9-21