Towards quantum computers that are robust to errors,b,b

For quantum computers to fulfil their potential, they need to detect and correct errors in encoded information to reach sufficiently low error rates for reliable operation. For the first time, a device has been created in which encoded error rates improve as the system size is increased.

This is a summary of: Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023).

为了让量子计算机充分发挥其潜力，它们需要检测和纠正编码信息中的错误，以达到足够低的错误率，以保证可靠的操作。首次创建了一种设备，其中随着系统规模的增加，编码错误率得到了改善。

这是 Google Quantum AI. Suppressing quantum errors by scaling a surface code logical qubit. Nature 614, 676–681 (2023) 的摘要。

The problem

Quantum algorithms are likely to have substantial impact in many fields, from chemistry, to physics, to mathematics. To bring the promise of quantum computers to reality, their qubits — the quantum analogue of classical bits — must be able to withstand noise, which can affect the accuracy of a quantum computer’s calculations. Qubits can exist in one of two states, and quantum noise can flip a qubit’s state, changing computational outcomes. In 1995, the first quantum-error-correcting code was proposed1, which was based on classical error-correcting codes used in the telecommunications industry. This discovery led to the development of several more error-correcting codes, including what are known as surface codes2, the focus of our work. Surface codes encode a logical qubit (a computational unit comprising multiple qubits) into the joint state of a 2D array of physical qubits. These codes increase error suppression as the array of physical qubits grows larger, as long as the noise experienced by the qubits is sufficiently below a noise threshold. Implementing these codes in the laboratory has been a major focus for years, but it has proved challenging to build a device that is large enough to handle the encoded information, while not exceeding the noise requirements above which error suppression ceases.

问题

量子算法可能在许多领域产生重大影响，从化学、物理到数学。为了使量子计算机的承诺变为现实，它们的量子比特（经典比特的量子模拟）必须能够承受噪声，这可能会影响量子计算机的计算准确性。量子比特可以存在于两种状态中，量子噪声可以翻转量子比特的状态，改变计算结果。1995年，首次提出了量子纠错码[1]，这是基于电信行业使用的经典纠错码的发现。这一发现导致了几种更多的纠错码的发展，包括我们工作的焦点——表面码[2]。表面码将逻辑量子比特（多个量子比特组成的计算单元）编码到2D物理量子比特阵列的联合状态中。只要量子比特所经历的噪声足够低于噪声阈值，这些码随着物理量子比特阵列的增大而增加误差抑制。多年来，在实验室中实现这些码一直是一个主要的焦点，但是建立一个足够大以处理编码信息的设备，同时不超过噪声要求，即上面超过误差抑制，已经被证明是具有挑战性的。

The solution

We created an expanded Sycamore device, a superconducting quantum processor with 72 qubits, by combining experimental hardware technologies to improve its quality over that of previous generations. We used this processor to support two surface codes: distance-5, a larger surface code encoded on 49 physical qubits, and the smaller distance-3, encoded on 17 physical qubits (Fig. 1a). We focused on surface codes because they are amenable to our device’s architecture, in which qubits communicate with their nearest neighbours, and because surface codes have a higher noise threshold than do other codes. Creating quantum operations this robust required considerable improvement of our calibration techniques and an increased understanding of the device’s physics, as well as improved algorithms for identifying which kinds of error had occurred during the error-correction process.

解决方案

我们通过结合实验硬件技术来改进其质量，创造了一个扩展的Sycamore设备，即72量子比特的超导量子处理器。我们使用这个处理器支持了两个表面码：距离-5，一个编码在49个物理量子比特上的较大表面码，以及距离-3，编码在17个物理量子比特上的较小表面码（图1a）。我们专注于表面码，因为它们适合我们设备的架构，在该架构中，量子比特与其最近的邻居通信，并且表面码的噪声阈值比其他码更高。创建如此强大的量子操作需要我们大量改进校准技术和对设备物理的理解，以及改进识别哪种错误发生在纠错过程中的算法。

Figure 1 | Reducing errors in a quantum processor. a, A schematic of the Sycamore device. Qubits that store information are shown as gold circles, and qubits that detect errors are shown as blue circles. Unused qubits are shown in grey. The area shaded blue indicates the logical qubit encoded by the large distance-5 surface code, which was compared with four averaged logical qubits encoded by the smaller distance-3 code (one ‘quadrant’ is outlined in red). Operations on the encoded qubit are shown in black (ZL) and green (XL). b, Logical-error probability for different numbers of error-correction rounds, as well as results from simulations (dotted curves), for the larger (blue) and smaller (red, averaged; pink, individual quadrants) logical qubits. The larger code (distance (d) = 5) had a lower error rate. c, Error rates with distance-5 codes (ε5) reduced more as the system improved (light to dark shading) than did error rates with distance-3 codes (ε3; individual quadrants and averages in open and filled circles, respectively). If ε5 and ε3 had improved equally, the dots would be along the red line.Credit: Google Quantum AI Nature (CC BY 4.0)

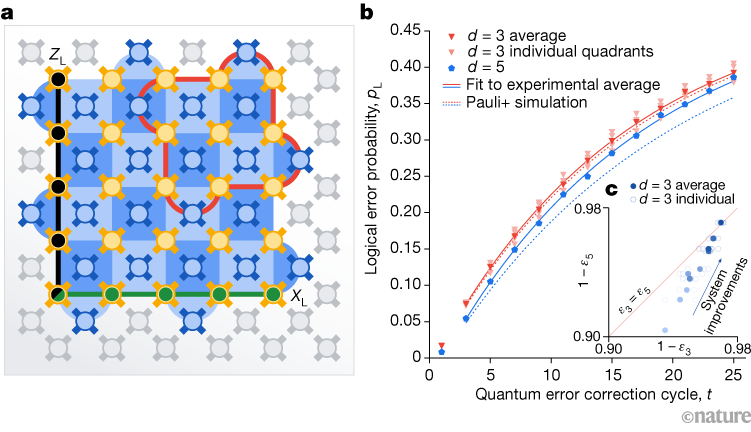
图1 | 减少量子处理器中的错误。 a，Sycamore设备的示意图。存储信息的量子比特显示为金色圆圈，检测错误的量子比特显示为蓝色圆圈。未使用的量子比特以灰色显示。阴影部分显示为大距离-5表面码编码的逻辑量子比特，它与较小的距离-3码编码的四个平均逻辑量子比特进行比较（其中一个“象限”用红色轮廓线标出）。编码量子比特的操作以黑色（ZL）和绿色（XL）显示。b，不同纠错周期的逻辑误差概率，以及模拟结果（虚线曲线），对较大（蓝色）和较小（红色，平均值；粉色，单个象限）逻辑量子比特的结果。较大的码（距离d=5）具有更低的错误率。c，距离-5码的误差率（ε5）随着系统的改进（从浅到深的阴影）而降低，而距离-3码的错误率（ε3；单个象限和平均值以开放和填充圆圈表示）并没有降低。如果ε5和ε3同样改善，这些点将沿着红线。来源：Google Quantum AI Nature (CC BY 4.0)

With these improvements, we found that the larger surface code enabled better logical-qubit performance (2.914% logical errors per cycle) than did the smaller surface code (3.028% logical error per cycle), as in Figure 1b. This indicates that we are approaching a regime in which low error rates are possible in quantum processors.

通过这些改进，我们发现较大的表面码使逻辑量子比特的性能更佳（每个周期2.914%的逻辑错误）比较小的表面码（每个周期3.028%的逻辑错误），如图1b所示。这表明我们正在接近一种低误差率在量子处理器中实现的情况。

Future directions

Quantum error correction will be a necessity for reducing error rates to a level that will enable quantum computing to realize its full potential. Previous experiments have run small quantum-error-correcting codes34, but their performance has never reached the point at which scaling the system size up would improve performance. In this work, we present not only the first encoded distance-5 logical qubit, but also the first chip in which the performance is actually at a level at which such improvement in scale is beneficial.

It is known in the field that, when the physical error rate of qubits is high, the probability of logical error increases with increasing system size, whereas when physical error rates are low, increasing the system size leads to the desired exponential suppression of logical error. We feel that we are currently in a ‘crossover’ regime between these scenarios, in which increasing system size initially suppresses the logical error per cycle, but would, with increasing size, later increase error rates. Therefore, it is imperative that we continue to improve both qubit performance and system scale.

There are two clear next steps on the path to fault-tolerant quantum computation: we must continue to aim for lower error rates, and we must begin to experimentally implement operations on these encoded logical qubits. Work on this second point has already begun5, but has yet to be demonstrated for our particular choice of architecture. Optimizing these methods will be crucial to implementing the quantum algorithms of the future. — Dripto M. Debroy is at Google Quantum AI, Los Angeles, California, USA.

Expert opinion

This is an impressive and important piece of work which, for the first time, tries to lower the logical error rate of a qubit encoded in a ‘fully quantum’ code by adding more redundancy. The main result is that the logical error rate per cycle of the distance-5 code is estimated to be slightly less than the average of the distance-3 codes. — Barbara Terhal is at the Delft University of Technology, Delft, the Netherlands.

Behind the paper

When we cooled this chip to superconducting temperatures, we were unsure about its performance, owing to some untested changes. It yielded almost perfectly, including fitting the distance-5 surface code, but we realized that this chip would need to be operated near-optimally to reach the performance level necessary for this demonstration. However, for unknown reasons, its initial performance was surprisingly poor. Over a couple of months, we learnt to control some subtle dynamics in the chip, dramatically improving its performance (Fig. 1c). As the qubit error rates fell, the larger code’s logical error rate caught up with that of the smaller code, because the larger code was more sensitive than the smaller code to improvements in qubit error rates. Figure 1c is inspired by a plot that we updated regularly to track improvements while working on the chip. One of our favourite parts of the experiment was adding the new points to the graph and seeing the larger code narrow the gap. — D.M.D.

From the editor

Although the route towards a fully error-corrected quantum computer has been laid out in theory, huge engineering challenges remain. By demonstrating that current superconducting circuit technology clears a key requirement for functioning error correction, this work represents a milestone for the development of future quantum computers. — Federico Levi, senior editor and team manager, Nature

未来的方向

量子纠错将是降低错误率以实现量子计算机的全部潜力所必需的。以前的实验运行了小规模的量子纠错码[3]，[4]，但它们的性能从未达到扩大系统规模将会提高性能的点。在这项工作中，我们不仅提出了第一个编码距离-5的逻辑量子比特，还提出了第一个芯片，其性能实际上已经达到了这种规模上的改进所需的水平。

在该领域已知，当量子比特的物理错误率很高时，逻辑错误的概率会随着系统规模的增加而增加，而当物理错误率很低时，增加系统规模会导致期望的指数逻辑错误抑制。我们认为，我们当前处在这些情况之间的“交叉”区域，其中增加系统规模最初会抑制每个周期的逻辑错误，但是随着规模的增加，会增加错误率。因此，我们必须继续改进量子比特性能和系统规模。

在通向容错量子计算机的道路上，有两个明确的下一步：我们必须继续朝着更低的错误率发展，并且我们必须开始在这些编码逻辑量子比特上实验性地实施操作。这个第二点的工作已经开始[5]，但尚未针对我们特定的架构进行演示。优化这些方法对于实现未来的量子算法至关重要。-Dripto M. Debroy在Google Quantum AI，加利福尼亚州洛杉矶。

专家意见

这是一项令人印象深刻且重要的工作，它首次尝试通过添加更多的冗余来降低完全量子编码中编码的逻辑错误率。主要结果是，距离-5码的逻辑错误率估计略低于距离-3码的平均值。-Barbara Terhal位于荷兰代尔夫特理工大学。

本文背后的故事

当我们将这个芯片冷却到超导温度时，由于一些未经测试的变化，我们对其性能并不确定。它几乎完美地适应了距离-5表面码，但我们意识到，为了达到此演示所需的性能水平，该芯片需要在接近最优的状态下运行。但是，由于未知的原因，其初始性能出乎意料地差。几个月后，我们学会了控制芯片中的一些微妙动态，大大提高了其性能（图1c）。随着量子比特误差率的降低，较大的码的逻辑错误率追赶上了较小码的逻辑错误率，因为较大的码比较小的码更敏感于量子比特误差率的改善。图1c受到我们定期更新以跟踪改进的启示，而我们最喜欢的实验部分之一是添加新点到图形中，看到更大的码缩小差距。-D.M.D.

来自编辑的话

虽然实现完全容错量子计算机的路线已经在理论上奠定，但仍存在巨大的工程挑战。通过展示当前超导电路技术清除了实现错误修正所需的关键要求，这项工作代表了未来量子计算机发展的一个里程碑。-Federico Levi，Nature高级编辑和团队经理

Towards quantum computers that are robust to errorsbb