GPT on a Quantum Computer | NotionNext BLOG

https://arxiv.org/html/2403.09418v1

一句话总结：本文探索了将ChatGPT的基础架构——转换器架构（Transformer architecture）应用于量子计算的可能性，旨在通过量子算法增强大型语言模型（LLMs）的效率和能力，为量子机器学习（QML）和人工智能技术的发展开辟新途径。

文章的观点:

大型语言模型（如ChatGPT）与量子机器学习（QML）的结合处于初级阶段，但已显示出巨大的研究潜力和应用前景。

通过详细设计量子电路以适应转换器架构的核心组件和生成预训练阶段，可以实现GPT在量子计算平台上的实现。

量子计算的整合旨在提升大型语言模型的功能，为量子机器学习（QML）和人工智能（AI）技术的演进做出贡献。

相关问题： 🤔Q: 为什么将大型语言模型（LLMs）与量子计算相结合是有前景的？ A: 量子计算提供了前所未有的计算能力，有潜力解决传统计算无法解决的复杂问题，将其与LLMs结合，可以增强模型的效率和处理能力。

🤔Q: 在量子计算平台上实现GPT的挑战有哪些？ A: 实现GPT的主要挑战包括设计能够适应量子计算环境的量子电路，以及适应其架构和预训练阶段的核心组件。

🤔Q: 将量子计算与LLMs结合的未来研究方向有哪些？ A: 未来的研究方向包括进一步探索量子算法在LLMs中的应用，优化和改进量子计算实现的效率，以及探索新的量子机器学习模型和技术。

这里是根据文章内容生成的关于在量子计算平台上实现GPT的思维导图：

此思维导图总结了文章的主要内容，包括LLMs与QML的结合、在量子计算平台上实现GPT的挑战以及未来的研究方向。

HTML conversions sometimes display errors due to content that did not convert correctly from the source. This paper uses the following packages that are not yet supported by the HTML conversion tool. Feedback on these issues are not necessary; they are known and are being worked on.

failed: graphpap

failed: shellesc

Authors: achieve the best HTML results from your LaTeX submissions by following these best practices.

Yidong Liao [email protected] Centre for Quantum Software and Information, University of Technology Sydney, Sydney, NSW, Australia Sydney Quantum Academy, Sydney, NSW, Australia [email protected] Centre for Quantum Software and Information, University of Technology Sydney, Sydney, NSW, Australia

(March 14, 2024)

Abstract

Large Language Models (LLMs) such as ChatGPT have transformed how we interact with and understand the capabilities of Artificial Intelligence (AI). However, the intersection of LLMs with the burgeoning field of Quantum Machine Learning (QML) is only in its nascent stages. This paper presents an exploration of this niche by detailing a comprehensive framework for implementing the foundational Transformer architecture — integral to ChatGPT — within a quantum computing paradigm. We meticulously design quantum circuits that implement adapted versions of the transformer’s core components and the generative pre-training phase. By integrating quantum computing with LLMs, we aspire to open new avenues for research in QML and contribute to the ongoing evolution of AI technologies.

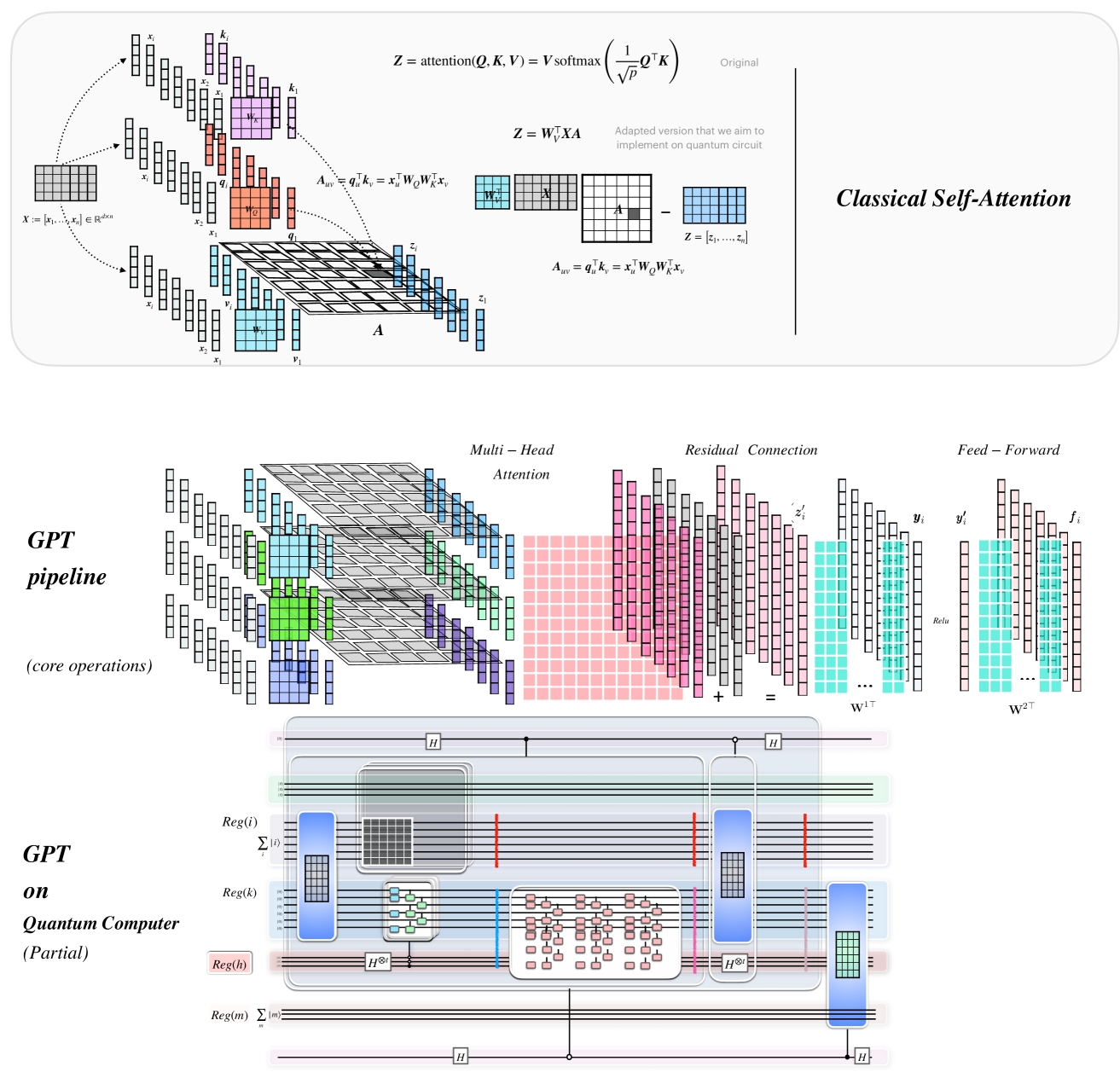
Figure 1: Preview of some key contents in this paper. Graphical representations of the classical Self-Attention Mechanism, GPT pipeline, and overall quantum implementation of GPT.

Contents

1 Introduction

2 Background

3 GPT on a Quantum Computer

4 Conclusion

1 Introduction

The emergence and rapid advancement of Large Language Models (LLMs) such as ChatGPT has had a significant global impact, revolutionizing our interactions with artificial intelligence and expanding our understanding of its capabilities. Models like GPT-4 have demonstrated the vast potential of LLMs in a wide range of applications across various domains. In the field of natural language processing (NLP), LLMs have proven to be highly proficient in tasks such as machine translation, sentiment analysis, question answering, and text summarization. They excel in identifying intricate language patterns, comprehending context, and generating text that is coherent and contextually appropriate.

Concurrently, the field of quantum computing has seen remarkable progress, offering unprecedented computational power that promises to solve complex problems beyond the reach of classical computing Scholten et al. (2024). Quantum Machine Learning (QML), an intersection of quantum computing and machine learning, has emerged as a fertile ground for research, aiming to leverage quantum algorithms to enhance machine learning tasks Cerezo et al. (2022). Despite the significant achievements in QML, integrating quantum computing with state-of-the-art machine learning models, especially LLMs, is only at its nascent stages. Recent explorations such as Ref. Liu et al. (2024); Gao et al. (2023) indicate a burgeoning interest in leveraging quantum computing to elevate the capabilities of LLMs.

This paper delves into the quantum implementation of Generative Pre-trained Transformer (GPT) Radford et al. (2018) (also referred to as GPT-11) — the original version of ChatGPT, focusing on adapting its architecture and pre-training processes to leverage the computational paradigms of quantum computing. We explore how quantum algorithms can be applied to the foundational components of GPT’s architecture and the generative pre-training, with the potential to enhance its efficiency and capabilities. By integrating quantum computing with LLMs, we aspire to open new avenues for research in QML and contribute to the ongoing evolution of AI technologies.

The rest of this paper is organized as follows: Section 2 provides a background on the transformer architecture used in GPT and the basics of language modeling. Section 3 details our approach to implement GPT’s architecture on quantum computers, including the quantum circuit designs for key model components and the generative pre-training. Section 4 concludes the paper with a summary of our findings and directions for future research.

2 Background

2.1 Transformer Architecture Used in GPT

The Generative Pre-trained Transformer (GPT) Radford et al. (2018) is the inaugural version in the series of groundbreaking language models developed by OpenAI, marking the beginning of a new era in NLP. GPT’s architecture is predicated on the transformer model Vaswani et al. (2017), a type of neural network that relies on self-attention mechanisms to process sequences of data, such as text. With 117 million parameters, GPT was a large model for its time, capable of capturing complex language patterns and generating coherent and contextually relevant text. GPT’s introduction was a pivotal moment in NLP; it paved the way for the development of more advanced models, such as GPT-2 and GPT-3, setting the stage for the rapid advancement of AI technologies in the years that followed. The remainder of this section gives an overview of GPT’s architecture and its training, and the next section 2.2 presents its application in language modeling.

Refer to caption

GPT’s architecture is a multi-layer decoder-only Transformer Liu et al. (2018) (a variant of the TransformerVaswani et al. (2017)). The primary part of the architecture is a stack of transformer blocks Radford et al. (2018), each of which is composed of two main components: a (masked) multi-head self-attention mechanism followed by a position-wise fully connected feed-forward network. Layer Normalization and Residual Connections are placed around these two main components. The transformer blocks are stacked on top of each other, with each layer processing the output of the previous one. Prior to the input embedding entering the transformer blocks, positional encoding is added. Fig.2 illustrates these components in GPT’s architecture, the following paragraphs briefly2 introduce each component.

Multi-Head Masked Self-Attention Mechanism

. The multi-head self-attention mechanism, with the addition of a masking operation, is a core component of the transformer block in GPT. This attention mechanism allows a model to weigh the importance of different words in a sentence. Unlike previous models (such as Recurrent Neural Networks(RNNs) Medsker and Jain (1999)) that process words in a sequential manner, self-attention enables the model to look at all parts of the sentence simultaneously. This allows for a more nuanced understanding of context and relationships between words, regardless of their position in the sentence. The masking operation is a critical aspect of this mechanism, especially in the context of language modeling(a brief introduction is given in Section 2.2): it ensures that the prediction of a current word does not get influenced by future words. Ghojogh and Ghodsi (2020)

Layer Normalization and Residual Connections

. Each transformer block in GPT includes layer normalization and residual connections. Layer Normalization is applied after the self-attention mechanism and after the feed-forward network within each transformer block. It normalizes the inputs across the features, improving the stability of the model. Residual Connections allow the input of each sub-layer (i.e., the self-attention and feed-forward networks) to be added to its output.

Position-Wise Fully Connected Feed-Forward Network

. In each transformer block in GPT, after the attention mechanism together with corresponding Layer Normalization and Residual Connection, the output is passed through a feed-forward network that applies the same transformation to each position separately and identically.

Positional Encoding

. Since GPT (and transformer models in general) does not inherently process sequential data in order, it uses positional encodings to incorporate information about the order of the sequence into its inputs. These positional encodings are added to the input embeddings at the bottom of the model stack, providing the model with information about the position of each word in the sequence.

The training process of GPT consists of two main stages Radford et al. (2018): unsupervised pre-training and supervised fine-tuning. During pre-training, GPT is exposed to a large corpus of text data, learning the underlying structure of the language without any task-specific instructions. This stage allowed the model to develop a broad understanding of language, including grammar, semantics, and common phrases. The fine-tuning stage then adapted the pre-trained model to specific tasks, such as translation, question-answering, and summarization, by training it on smaller, task-specific datasets.

2.2 Language Modeling basics

This section briefly introduces one of GPT’s applications in language modeling — text generation, which is the foundation of the services provided by ChatGPT. We start by presenting an overview of language modelling:

Language modeling is a fundamental aspect of natural language processing (NLP) that focuses on the development of probabilistic models capable of understanding, generating, and interpreting human language. At its core, a language model predicts the likelihood of upcoming sequences of words occurring in a text Jurafsky and Martin (2021). This predictive capability enables a wide range of applications, from autocomplete systems in smartphones and email platforms to sophisticated chatbots, machine translation, speech recognition, and even content generation tools.

The essence of language modeling lies in capturing the statistical structure of language—learning how words and phrases tend to come together to convey meaning. Early language models were relatively simple n-gram modelsBrown et al. (1992), where the prediction of the next word in a sequence depended on the previous n−1 words. However, these models had limitations, particularly in dealing with long-term dependencies and the vast diversity of linguistic contexts. The advent of neural networks brought a significant leap forward in language modeling. Recurrent Neural Networks (RNNs)Medsker and Jain (1999), and later, Long Short-Term Memory (LSTM) networksHochreiter and Schmidhuber (1997), provided mechanisms to remember information over longer sequences, improving the model’s ability to handle context in language. Despite these advances, RNNs and LSTMs also faced challenges, such as difficulty in training over very long sequences and capturing complex dependencies.

The breakthrough came with the introduction of the Transformer architectureVaswani et al. (2017), which led to the development of models like OpenAI’s GPT series that demonstrated unprecedented capabilities in generating coherent and contextually relevant text over extended passages. The development of language models continues to be a vibrant area of research in AI, with ongoing work aimed at improving their accuracy, efficiency, and ability to understand and generate human language in all its complexity.

Next, we delve into fundamental concepts of language modeling, such as tokenization, explaining how a language model (here, GPT) operates for text generation.

2.2.1 Tokenization, Word Embedding

Tokenization is the process of converting text into tokens which are the basic units of language models. There are three levels of tokenization:

Character-level: Processes text one letter at a time.

Word-level: Segments text into individual words.

Subword-level: Breaks down words into subunits. For example, the subword tokenization of the phrase ”Language Model” may look like [”Lan”, ”gu”, ”age ”, ”Mod”, ”el”].

Upon establishing the tokens for a language model, we arrange them into a structured vocabulary, assigning a distinct index to each token. These indices are then transformed into input features through various methodologies. Directly inputting these indices into the model is inadvisable, as the sequential order within the vocabulary does not inherently reflect semantic relationships. An alternative is the utilization of one-hot encoding. For a vocabulary encompassing 10,000 words, each word is symbolized by a 10,000-element vector, predominantly composed of zeros, save for the element corresponding to the word’s indexed position. The primary benefit of one-hot encoding is its ability to preclude presumptions about word importance, facilitating the model’s learning of word relationships during its training phase.

However, one-hot encoding presents scalability issues in the context of extensive vocabularies. Considering the English language, with its repertoire exceeding 100,000 words, representing a single word would necessitate a vector comprising 100,000 elements. In scenarios involving lengthy sequences, this approach demands substantial storage space and computational resources. To mitigate this issue of dimensionality, the use of word embeddings is proposedMikolov et al. (2013); Pennington et al. (2014); Goldberg and Levy (2014); Mikolov et al. (2015). In this framework, an embedding layer projects the one-hot encoded tokens into a more condensed vector space. These embeddings, essentially denser token representations, are generated through a linear layer equipped with a weight matrix, which the model optimizes during its training process. Fig.3 summarizes this section.

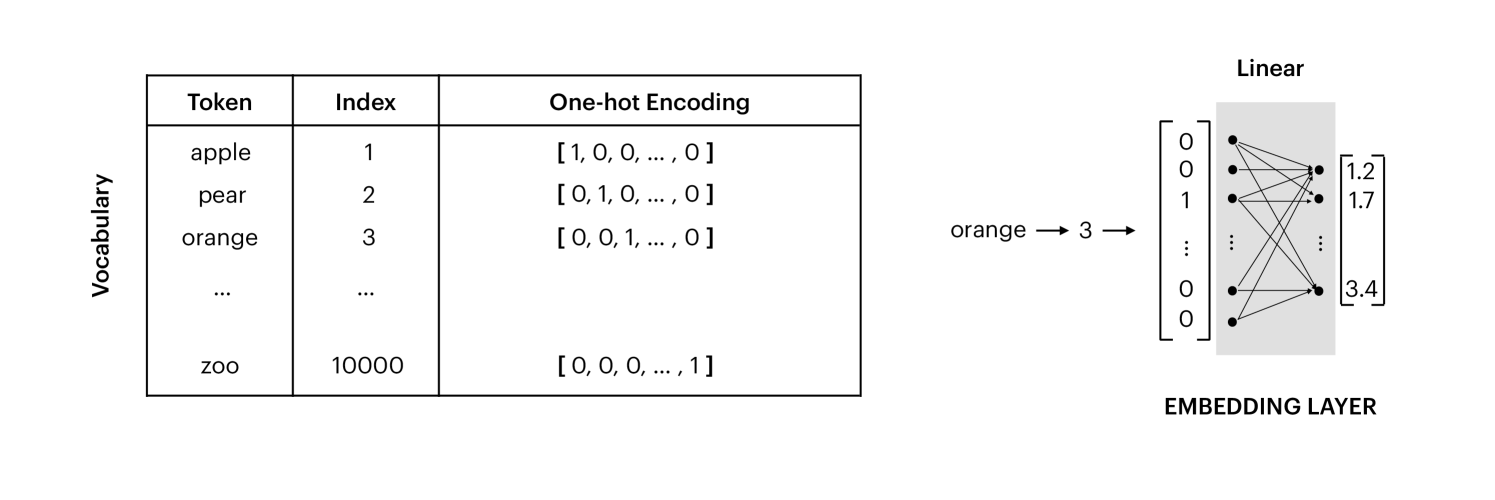
Figure 3: Tokenization, one-hot encoding and word embedding.

2.2.2 Next word prediction

In the inference stage, a language model (here, GPT) takes in a sequence of one-hot encoded tokens, and generates predictions for the next word in a sequence.3 The sequence of one-hot encoded tokens is first transformed through word embedding, as described in the above section. These embeddings, after the positional encodings are added, are then input into the transformer blocks. Then, a final linear layer is applied to map the outputs from the transformer blocks back into the vocabulary space, generating a sequence of transformed vectors. The last transformed vector in the sequence is referred as ”logits”. The logits are passed through a softmax activation function, yielding a probability distribution across the vocabulary, indicating the likelihood of each word as the next sequence component. Fig.4 summarizes this section.

Refer to caption

2.2.3 Generative Pre-training

GPT model undergo extensive pre-training on large text corpora using the following loss function:

ㅤ

L⁢(θ)=−∑tlog⁡P⁢(wt|w1:t−1;θ)

ㅤ

(1)

where wt is the t-th word, and θ represents the model parameters. This pre-training endows GPT with a broad understanding of language, which is then refined for specific tasks through fine-tuning.

Given the unlabeled nature of these sentences, this process is classified as unsupervised learning. It involves the pairing of a text segment as input with its subsequent segment as the target. The training process encompasses processing these input-target pairs in batches. The loss is computed by evaluating the next token in the target output, and this process is repeated for each subsequent token in the sequence. The cumulative loss is calculated across all batches, followed by the execution of backpropagation to adjust the model’s parameters.

The culmination of this process is a pre-trained language model, which we can then employ for text generation. This begins with the input of an initial word or phrase, serving as the genesis for text generation. The model assesses this input to predict the next token, which is subsequently reintroduced into the model as the new input. This iterative process engenders a feedback loop, enabling the model to generate continuous text sequences.

3 GPT on a Quantum Computer

As outlined in Section 2.1 and depicted in Figure 2, the architecture of GPT encompasses several key elements: input embedding, positional encoding, a series of transformer blocks, and a concluding linear layer followed by a softmax function. Within the context of this paper, it is assumed that both the input embedding and positional encoding are executed on classical computers. Our focus, however, shifts to detailing the implementation of the transformer blocks’ core components on a quantum computer. Additionally, we delve into the methodologies employed for executing Generative Pre-training of the model on a quantum computer. To ensure a holistic presentation, a detailed exposition on the quantum implementation of positional encoding is provided in Appendix B.

3.1 Input encoding

In this section, we focus on the process of input encoding for the quantum implementation of a Transformer block. As illustrated in Figure 4, the input to the Transformer block is a sequence of vectors {𝒙i∈ℝd}i=1n stacked as a matrix 𝑿:=[𝒙1,…,𝒙n]∈ℝd×n. It can be encoded in a quantum state (after normalization4) |ψ𝑿⟩ as,

ㅤ

|ψ𝑿⟩:=∑i=1n|i⟩⁢|𝒙i⟩,

ㅤ

(2)

where |𝒙i⟩:=∑k=1d𝒙i(k)⁢|k⟩ is the amplitude encoding of the vector 𝒙i whose k-th elements are denoted as 𝒙i(k).

The entire state is prepared on two quantum registers hosting the index k and index i, which are denoted as R⁢e⁢g⁢(k) and R⁢e⁢g⁢(i), respectively. The unitary that realizes the data encoding as,

ㅤ

U𝑿:|i⟩⁢|0⟩→|i⟩⁢|𝒙i⟩,∀i=1,⋯⁢n,

ㅤ

(3)

is represented as the blue box in Fig.6. U𝑿 can be achieved by “Controlled Quantum State Preparation(CQSP)” process Yuan and Zhang (2023).

3.2 Attentions on Quantum Computer

As mentioned in Section. 2.1, the multi-head self-attention, with the addition of a masking operation, is a core component of the transformer block in GPT. In this section, we present the quantum implementation of an adapted version of this component: Subsection. 3.2.1 illustrates the adaptation of single-head self-attention and its implementation on quantum computers, while Subsection. 3.2.2 discusses multi-head self-attention and its implementation on quantum computers. The masking operation and its quantum implementation are given in Appendix. C.

In classical transformer architecture, the attention function can be described as mapping queries, keys, and values to an output, where the queries, keys, values, and output are all vectors Vaswani et al. (2017). The query 𝒒i, key 𝒌i, and value 𝒗i are p-dimensional, p-dimensional, and r-dimensional vectors defined as Ghojogh and Ghodsi (2020):

ㅤ	ℝp∋𝒒i=𝑾Q⊤⁢𝒙i,	ㅤ	(4)
ㅤ	ℝp∋𝒌i=𝑾K⊤⁢𝒙i,	ㅤ	(5)
ㅤ	ℝr∋𝒗i=𝑾V⊤⁢𝒙i,	ㅤ	(6)

where 𝑾Q∈ℝd×p,𝑾K∈ℝd×p, and 𝑾V∈ ℝd×r are trainable matrices.5 Similar to vectors {𝒙i∈ℝd}i=1n being stacked as a matrix 𝑿:=[𝒙1,…,𝒙n]∈ℝd×n, we define 𝑸:=[𝒒1,…,𝒒n]∈ℝp×n, 𝑲:=[𝒌1,…,𝒌n]∈ℝp×n, and 𝑽:=[𝒗1,…,𝒗n]∈ ℝr×n. From these definitions, we have

ㅤ	𝑸=𝑾Q⊤⁢𝑿,	ㅤ	(7)
ㅤ	𝑲=𝑾K⊤⁢𝑿,	ㅤ	(8)
ㅤ	𝑽=𝑾V⊤⁢𝑿,	ㅤ	(9)

The ”Scaled Dot-Product Attention” defined in Vaswani et al. (2017) can be written in matrix form as:

ㅤ

𝒁0:=attention⁡(𝑸,𝑲,𝑽)=𝑽⁢softmax⁡(1p⁢𝑸⊤⁢𝑲),

ㅤ

(10)

where 𝒁0=[𝒛𝟎1,…,𝒛𝟎n]∈ℝr×n .

Note that for each i, the queries, keys, and values are all from the same vector 𝒙i in the sequence; this type of attention is referred to as the ”self-attention” Ghojogh and Ghodsi (2020).

Refer to caption

3.2.1 Self-Attention(single-head) on Quantum Computer

The ”Scaled Dot-Product Attention” defined in Eqn. 10 can also be written as follows by plugging in Eqn. 9 and denoting 𝑨0≡softmax⁡(1p⁢𝑸⊤⁢𝑲):

ㅤ

𝒁0=𝑾V⊤⁢𝑿⁢𝑨0

ㅤ

(11)

Considering it is not straightforward to implement the softmax function6using quantum circuit and the scaling will be taken care of in the block-encoding7 procedure described later in this section, we aim to implement an alternative version of 𝑨0 denoted as 𝑨≡𝑸⊤⁢𝑲, that is, we aim to design quantum circuit implementing the following computation:

ㅤ

𝒁=𝑾V⊤⁢𝑿⁢𝑨,

ㅤ

(12)

where 𝒁=[𝒛1,…,𝒛n]∈ℝr×n .

Note that the matrix elements of 𝑨 are

ㅤ

𝑨u⁢v=𝒒u⊤⁢𝒌v=𝒙u⊤⁢𝑾Q⁢𝑾K⊤⁢𝒙v

ㅤ

(13)

The above description of classical attention (the modified version that we aim to implement on the quantum circuit) can be illustrated in Fig.5. Next, we present its quantum implementation.

On a quantum circuit, after the input encoding described in 3.1, the attention function can be implemented by applying the block-encoding of 𝑨⊤ and a parameterized quantum circuit8 for 𝑾V⊤ on the two quantum registers R⁢e⁢g⁢(i) and R⁢e⁢g⁢(k) respectively, as depicted in Fig. 6.

Refer to caption

This can be proven as follows:

Starting from Eq. 12, we have

ㅤ

𝒁=𝑾V⊤⁢𝑿⁢𝑨,

ㅤ

Utilizing the formula 𝑣𝑒𝑐⁢(A⁢B⁢C)=(C⊤⊗A)⁢𝑣𝑒𝑐⁢(B), we obtain

ㅤ

𝑣𝑒𝑐⁢(𝒁)=𝑣𝑒𝑐⁢(𝑾V⊤⁢𝑿⁢𝑨)=(𝑨⊤⊗𝑾V⊤)⁢𝑣𝑒𝑐⁢(𝑿).

ㅤ

(14)

For a matrix M, defining vectors 𝝍𝑴=𝑣𝑒𝑐⁢(M) transforms Eq. 14 into

ㅤ

𝝍𝒁=(𝑨⊤⊗𝑾V⊤)⁢𝝍𝑿.

ㅤ

(15)

Recall Eq. 2:

ㅤ

|ψ𝑿⟩=∑i=1n|i⟩⁢|𝒙i⟩,

ㅤ

where writing the quantum states in Eq. 2 as vectors yields

ㅤ

𝝍𝑿=|ψ𝑿⟩.

ㅤ

(16)

Correspondingly, we have

ㅤ

𝝍𝒁=|ψ𝒁⟩,

ㅤ

(17)

From Eq. 17 to Eq. 15, we derive

ㅤ

|ψ𝒁⟩=(𝑨⊤⊗𝑾V⊤)⁢|ψ𝑿⟩.

ㅤ

(18)

This corresponds to the action of the quantum circuit for self-attention, which can be represented as

ㅤ

|ψ𝒁⟩⊗|0⟩+…=(U𝑨⊤⊗U𝑾V⊤)⁢(|ψ𝑿⟩⊗|0⟩),

ㅤ

(19)

where U𝑨⊤ corresponds to applying the block-encoding of 𝑨⊤, and U𝑾V⊤ is a parameterized quantum circuit implementing 𝑾V⊤ on the two quantum registers R⁢e⁢g⁢(i) and R⁢e⁢g⁢(k) respectively. The term ”+…”9 indicates that upon post-selecting, we can obtain the desired state |ψ𝒁⟩=𝑣𝑒𝑐⁢(𝒁).

The block-encoding of 𝑨⊤ can be constructed using the following lemma from Ref. Nguyen et al. (2022).

Lemma 3.2 from Ref. Nguyen et al. (2022) (Naive block-encoding of dense matrices with oracle access). Let A∈ℂN×N (where N=2s) with ai⁢j being its elements and let a^⩾maxi,j⁡|ai⁢j|. Suppose the following oracle is provided

ㅤ

OA:|i⟩⁢|j⟩⁢|0⟩⊗b→|i⟩⁢|j⟩⁢|a~i⁢j⟩,

ㅤ

where 0⩽i,j<N and a~i⁢j is the (exact) b-qubit description of ai⁢j/a^. Then one can implement a (N⁢a^,s+1,ϵ)-block-encoding of A with two uses of OA, O⁢(polylog⁢(a^⁢N/ϵ)) one- and two-qubit gates and O⁢(b,polylog⁢(a^⁢N/ϵ)) extra qubits (which are discarded before the post-selection step).

Below we explain how the block-encoding of 𝑨⊤∈ℝn×n can be constructed using the above lemma:

From Eqn.13, the matrix elements of 𝑨⊤ (which we denote as Λi⁢j) are

ㅤ

Λi⁢j:=𝑨⊤i⁢j=𝒙j⊤⁢𝑾Q⁢𝑾K⊤⁢𝒙i

ㅤ

(20)

let Λ^⩾maxi,j⁡|Λi⁢j| and Λ~i⁢j is defined to be the (exact) b-qubit description of Λi⁢j/Λ^.

According to the above lemma, we need the following oracle to the block-encoding of 𝑨⊤

ㅤ

O𝑨⊤:|i⟩⁢|j⟩⁢|0⟩⊗b→|i⟩⁢|j⟩⁢|Λ~i⁢j⟩,

ㅤ

(21)

where 0⩽i,j<n.

This oracle O𝑨⊤ can be constructed in the same way as constructing O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇 (described in Appendix A) defined in Eqn.72 with the attention score as Eqn.73. Therefore, substituting A in the above lemma with 𝑨⊤, we can implement the block-encoding of 𝑨⊤ with two uses of O𝑨⊤, O⁢(polylog⁢(Λ^⁢n/ϵ)) one- and two-qubit gates.

3.2.2 Multihead-Attention on Quantum computer

In the multihead attention module, We have H set of queries, values, and keys as Ghojogh and Ghodsi (2020):

ㅤ	ㅤ	ℝp×n∋𝑸h=𝑾Q,h⊤⁢𝑿,∀h∈{1,…,H},	ㅤ
ㅤ	ㅤ	ℝp×n∋𝑽h=𝑾V,h⊤⁢𝑿,∀h∈{1,…,H},	ㅤ
ㅤ	ㅤ	ℝr×n∋𝑲h=𝑾K,h⊤⁢𝑿,∀h∈{1,…,H}.	ㅤ

Then, the scaled dot product attention is applied to generate the H output {𝒁h}h=1H, in accordance with Eqn.12:

ㅤ

𝒁h=𝑾V,h⊤⁢𝑿⁢𝑨h,

ㅤ

(22)

where 𝑨h≡𝑸h⊤⁢𝑲h, and 𝒁h=[𝒛1,h,…,𝒛n,h]∈ℝr×n.

The outputs are concatenated over different heads as

ㅤ

𝒁Multi-heads=[∥h=1H𝒛1,h,∥h=1H𝒛2,h,…,∥h=1H𝒛n,h,]∈ℝr⁢H×n

ㅤ

(23)

where ∥ represents concatenation Velickovic et al. (2017). Then, by a linear projection 𝑾O⊤, the total attention value is obtained:

ㅤ

𝒛i𝖳𝗈𝗍𝖺𝗅:=𝑾O⊤∥h=1H⁢𝒛i,h

ㅤ

(24)

ㅤ

𝒁𝖳𝗈𝗍𝖺𝗅:=𝑾O⊤⁢𝒁Multi-heads

ㅤ

and 𝒁𝖳𝗈𝗍𝖺𝗅=[𝒛1𝖳𝗈𝗍𝖺𝗅,…,𝒛n𝖳𝗈𝗍𝖺𝗅]∈ℝr⁢H×n.

The above description of classical multihead attention can be illustrated in Fig.7. Next, we present its quantum implementation.

Refer to caption

On a quantum circuit, we aim to obtain the following quantum state,

ㅤ

|ψ𝒁𝖳𝗈𝗍𝖺𝗅⟩:=∑i=1n|i⟩⊗|𝒛i𝖳𝗈𝗍𝖺𝗅⟩

ㅤ

(25)

where |𝒛i𝖳𝗈𝗍𝖺𝗅⟩ is the amplitude encoding of the vector 𝒛i𝖳𝗈𝗍𝖺𝗅. This can be achieved via the quantum circuit depicted in Fig.7 in which the additional register R⁢e⁢g⁢(h) is hosting index h, and the multi-controlled unitary is defined as

ㅤ

UMulti-heads=∑h|h⟩⁢⟨h|⊗USingle-head

ㅤ

(26)

with USingle-head=(U𝑨h⊤⊗U𝑾V,h⊤) representing the block-encoding of 𝑨h⊤ and a parameterized quantum circuit for 𝑾V,h⊤ for each head.

For a single head, from Eq. 19, when USingle-head acts on the state |ψ𝑿⟩⊗|0⟩, the outcome state is

ㅤ

USingle-head⁢(|ψ𝑿⟩⊗|0⟩)=|ψ𝒁h⟩⊗|0⟩+…

ㅤ

(27)

where |ψ𝒁h⟩:=∑i=1n|i⟩⊗|𝒛i,h⟩ and |𝒛i,h⟩ is the amplitude encoding of the vector 𝒛i,h.

When UMulti-heads acts on the state prepared as ∑h|h⟩⊗(|ψ𝑿⟩⊗|0⟩) by the blue box and Hadamard gates on R⁢e⁢g⁢(h), the outcome state is

ㅤ

|ψMulti-heads⟩=UMulti-heads⁢(∑h|h⟩⊗(|ψ𝑿⟩⊗|0⟩))=∑h|h⟩⊗(|ψ𝒁h⟩⊗|0⟩+…)

ㅤ

(28)

upon post-selecting, we obtain the state

ㅤ	\|ψMulti-heads⟩=∑i=1n\|i⟩⊗∑h\|h⟩⁢\|𝒛i,h⟩	ㅤ	(29)
ㅤ	=∑i=1n\|i⟩⊗\|∥h=1H𝒛i,h⟩	ㅤ	(30)

where |∥h=1H𝒛i,h⟩ is the amplitude encoding of the vector ∥h=1H𝒛i,h.

Applying a parameterized quantum circuit implementing 𝑾O⊤ on R⁢e⁢g⁢(k) and R⁢e⁢g⁢(h), which act as U𝑾O⊤|∥h=1H𝒛i,h⟩=|𝒛i𝖳𝗈𝗍𝖺𝗅⟩, obtain

ㅤ	U𝑾O⊤\|ψMulti-heads⟩=∑i=1n\|i⟩⊗U𝑾O⊤\|∥h=1H𝒛i,h⟩	ㅤ	(31)
ㅤ	=∑i=1n\|i⟩⊗\|𝒛i𝖳𝗈𝗍𝖺𝗅⟩	ㅤ	(32)
ㅤ	=\|ψ𝒁𝖳𝗈𝗍𝖺𝗅⟩	ㅤ	(33)

which is the desired state in Eqn.25.

3.3 Residual-connection on Quantum computer

After the multihead attention module, the input to the transformer block 𝒙i and the total attention value 𝒛i𝖳𝗈𝗍𝖺𝗅 are added (often referred as ”residual-connection” introduced by ResNet He et al. (2016)):

ㅤ

𝒛i′:=𝒛i𝖳𝗈𝗍𝖺𝗅+concat⁡(𝒙i,𝒙i,…⁢𝒙i)∈ℝr⁢H

ㅤ

(34)

where concat⁡(𝒙i,𝒙i,…⁢𝒙i) represents the concatenation of H identical vectors10 𝒙i, For later use, define |concat⁡(𝒙i,𝒙i,…⁢𝒙i)⟩ as the amplitude encoding of the vector concat⁡(𝒙i,𝒙i,…⁢𝒙i) and 𝒁′:=[𝒛′1,…,𝒛′n]∈ℝr⁢H×n.

On the quantum circuit, we aim to obtain the following quantum state

ㅤ

|ψ𝒁′⟩:=∑i=1n|i⟩⊗|𝒛′i⟩

ㅤ

(35)

where |𝒛′i⟩ is the amplitude encoding of the vector 𝒛′i. This can be achieved via the quantum circuit depicted in Fig.8.

Refer to caption

The first transparent box controlled by the top ancillary qubit in Fig.8 implements U𝒁𝖳𝗈𝗍𝖺𝗅 which acts as

ㅤ

U𝒁𝖳𝗈𝗍𝖺𝗅:|i⟩⊗|0⟩→|i⟩⊗|𝒛i𝖳𝗈𝗍𝖺𝗅⟩

ㅤ

(36)

The blue box represents the data encoding (containing positional encoding) which acts as

ㅤ

U𝑿:|i⟩⊗|0⟩→|i⟩⊗|𝒙i⟩

ㅤ

(37)

Including the Hadamard gates, the second transparent box controlled by the top ancillary qubit acts on the input state as

ㅤ

U𝑿⊗H⊗t⁢(∑i=1n|i⟩⊗|0⟩⊗|0⟩)=∑i=1n|i⟩⊗|𝒙i⟩⊗∑h|h⟩=|ψ𝑿⟩⊗∑h|h⟩

ㅤ

(38)

where t=log2⁡(H), and the H here is the number of ”heads” in the multi-head attention defined in Section 3.2.2.

ㅤ	\|ψ𝒁𝖳𝗈𝗍𝖺𝗅⟩+\|ψ𝑿⟩⊗∑h\|h⟩	=∑i=1n\|i⟩⊗\|𝒛i𝖳𝗈𝗍𝖺𝗅⟩+∑i=1n\|i⟩⊗\|𝒙i⟩⊗∑h\|h⟩	ㅤ	(39)
ㅤ	ㅤ	=∑i=1n\|i⟩⊗(\|𝒛i𝖳𝗈𝗍𝖺𝗅⟩+\|𝒙i⟩⊗∑h\|h⟩)	ㅤ	ㅤ
ㅤ	ㅤ	=∑i=1n\|i⟩⊗(\|𝒛i𝖳𝗈𝗍𝖺𝗅⟩+∑h\|h⟩⁢\|𝒙i⟩)	ㅤ	ㅤ
ㅤ	ㅤ	=∑i=1n\|i⟩⊗(\|𝒛i𝖳𝗈𝗍𝖺𝗅⟩+\|concat⁡(𝒙i,𝒙i,…,𝒙i)⟩)	ㅤ	ㅤ
ㅤ	ㅤ	=∑i=1n\|i⟩⊗\|𝒛i′⟩=\|ψ𝒁′⟩.	ㅤ	ㅤ

which is the desired state in Eqn.35.

In our quantum implementation of GPT, the layer normalization procedure is omitted, our quantum approach leverages the inherent unitarity of quantum state evolutions to achieve normalization.

3.4 Feed-Forward Network on Quantum computer

After the multihead attention module and residual connection, a position-wise Feed-Forward Network(FFN) is appliedGhojogh and Ghodsi (2020). The FFN is a fully connected feed-forward module that operates separately and identically on each 𝒛i′:

ㅤ

FFN⁡(𝒛i′)=𝐖2⊤⁢ReLU⁡(𝐖1⊤⁢𝒛i′+𝐛1)+𝐛2,

ㅤ

where 𝐖1∈ℝr⁢H×df⁢f,𝐖2∈ ℝdf⁢f×r⁢H,𝐛1∈ℝdf⁢f,𝐛2∈ℝr⁢H are trainable parameters, df⁢f is the intermediate dimension of the FFN. For simplicity, we omit 𝐛1,𝐛2 in the following discussion. Similar to how we defined 𝑿:=[𝒙1,…,𝒙n] before, we can write 𝐖1=[𝒘1,…,𝒘m,…,𝒘df⁢f] where 𝒘m∈ℝr⁢H.

Denote 𝒚i:=𝐖1⊤⁢𝒛i′∈ℝdf⁢f, we have its elements as

ㅤ

𝒚i(m)=𝒛i′⋅𝒘m,∀m∈{1,…,df⁢f}

ㅤ

(40)

Refer to caption

Next, we present a quantum implementation of the FFN module similar to the approach proposed in Ref. Allcock et al. (2020).

Recall the unitary circled in the overall transparent box in Fig.8, denoted as U𝒁′, act as

ㅤ

U𝒁′:|i⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋→|i⟩⁢|𝒛′i⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋+…,∀i∈{1,⋯⁢n}.

ㅤ

(41)

where |0⟩k,h represents the ”all-zero” state 11 of the qubits in R⁢e⁢g⁢(k) and R⁢e⁢g⁢(h), |0⟩𝗈𝗍𝗁𝖾𝗋 represents the ”all-zero” state of the ancillary qubits(qubits that are not included in R⁢e⁢g⁢(i),R⁢e⁢g⁢(k),R⁢e⁢g⁢(h) in Fig.8).

For implementing 𝐖1:=[𝒘1,…,𝒘m,…,𝒘df⁢f], we can create a trainable unitary

ㅤ

U𝐖𝟏:|m⟩⁢|0⟩k,h→|m⟩⁢|𝒘m⟩,∀m∈{1,…,df⁢f}.

ㅤ

(42)

with |𝒘m⟩ on R⁢e⁢g⁢(k),R⁢e⁢g⁢(h) and |m⟩ on an additional registered R⁢e⁢g⁢(m).

Notice that

ㅤ

𝒚i(m)=⟨𝒛i′|𝒘m⟩,∀m∈{1,…,df⁢f}

ㅤ

(43)

This can be evaluated using parallel swap test for each 𝒛i′∈ℝr⁢H and 𝒘m∈ℝr⁢H, via the quantum circuit depicted in Fig.9.

The input state to the circuit is

ㅤ

|Ψ0⟩=∑i∑m|i⟩⁢|m⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩

ㅤ

(44)

For each branch |i⟩⁢|m⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩, applying a Hadamard gate on the bottom ancillary qubit, and controlled U𝒁′, U𝐖𝟏 we obtain

ㅤ

|i⟩⁢|m⟩⁢(|𝒛′i⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋+…)⁢|0⟩+|i⟩⁢|m⟩⁢|𝒘m⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|1⟩

ㅤ

(45)

Applying another Hadamard gate on the bottom ancillary qubit yield

ㅤ

|ψi⁢m⟩=|i⟩⁢|m⟩⁢((|𝒛′i⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋+…)+|𝒘m⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋)⁢|0⟩+|i⟩⁢|m⟩⁢((|𝒛′i⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋+…)−|𝒘m⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋)⁢|1⟩

ㅤ

(46)

((|𝒛′i⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋+…)−|𝒘m⟩⁢|0⟩𝗈𝗍𝗁𝖾𝗋) respectively.

Then there is a real number θi⁢m such that

ㅤ

|ψi⁢m⟩=|i⟩|m⟩(sinθi⁢m|ui⁢m⟩|0⟩+cosθi⁢m|vi⁢m⟩|1⟩)⏟∣ϕi⁢m⟩=|i⟩|m⟩|ϕi⁢m⟩

ㅤ

(47)

θi⁢m satisfies cos⁡θi⁢m=1−⟨𝒛i′|𝒘m⟩/2, sin⁡θi⁢m=1+⟨𝒛i′|𝒘m⟩/2, and we have:

ㅤ

⟨𝒛i′|𝒘m⟩=−cos⁡2⁢θi⁢m.

ㅤ

(48)

To summarize, the quantum circuit depicted in Fig.9, denoted as U, acts as

ㅤ

U:|i⟩|m⟩|0⟩k,h|0⟩𝗈𝗍𝗁𝖾𝗋|0⟩→|i⟩|m⟩(sinθi⁢m|ui⁢m⟩|0⟩+cosθi⁢m|vi⁢m⟩|1⟩)⏟∣ϕi⁢m⟩=|i⟩|m⟩|ϕi⁢m⟩,

ㅤ

(49)

where 𝒚i(m)=⟨𝒛i′|𝒘m⟩ are encoded as

ㅤ

⟨𝒛i′|𝒘m⟩=−cos⁡2⁢θi⁢m.

ㅤ

(50)

When acting on the input state to the circuit |Ψ0⟩=∑i∑m|i⟩⁢|m⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩, U , also depicted as the pink box in Fig.10, produces the following state

ㅤ

|Ψ1⟩=∑i∑m|i⟩|m⟩(sinθi⁢m|ui⁢m⟩|0⟩+cosθi⁢m|vi⁢m⟩|1⟩)⏟∣ϕi⁢m⟩=∑i∑m|i⟩|m⟩|ϕi⁢m⟩

ㅤ

(51)

Next use amplitude estimation Brassard et al. (2002) to extract and store 𝒚i(m)=⟨𝒛i′|𝒘m⟩ into an additional register which we call the “amplitude register” |0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t and the output state |Ψ1⟩ (using the same notation) becomes

ㅤ

|Ψ3⟩=∑i∑m|i⟩⁢|m⟩⁢|ϕi⁢m⟩⁢|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t,

ㅤ

(52)

where |ϕi⁢m⟩ can be decomposed as

ㅤ

|ϕi⁢m⟩=−i2⁢(ei⁢θi⁢m⁢|ω+⟩i⁢m−ei⁢(−θi⁢m)⁢|ω−⟩i⁢m).

ㅤ

(53)

where |w±⟩i⁢m=12⁢(|0⟩⁢|ui⁢m⟩±𝒊⁢|1⟩⁢|vi⁢m⟩).

Hence, we have

ㅤ

|Ψ1⟩=∑i∑m−i2⁢(ei⁢θi⁢m⁢|i⟩⁢|m⟩⁢|ω+⟩i⁢m−ei⁢(−θi⁢m)⁢|i⟩⁢|m⟩⁢|ω−⟩i⁢m)⁢|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t.

ㅤ

(54)

The overall Grover operator G is defined as

ㅤ

G≔U⁢C2⁢U−1⁢C1,

ㅤ

(55)

where C1 is the Z gate on the bottom ancilla qubit in the pink box, and C2=(I−2⁢|0⟩⁢⟨0|)⊗Ii,m is the “flip zero state” on registers other than R⁢e⁢g⁢(i),R⁢e⁢g⁢(m) (represented as S0 in Fig.10).

Utilising Eqn. 49, it can be shown that G can be expressed as

ㅤ

G=∑i∑m|i⟩|m⟩⟨m|⟨i|⊗Gi⁢m,

ㅤ

(56)

where Gi⁢m is defined as

ㅤ

Gi⁢m=(I−2|ϕi⁢m⟩⟨ϕi⁢m|))(Z⊗I)

ㅤ

(57)

It is easy to check that |w±⟩i⁢m are the eigenstates of Gi⁢m, that is,

ㅤ

Gi⁢m⁢|w±⟩i⁢m=e±𝒊⁢2⁢θi⁢m⁢|w±⟩i⁢m.

ㅤ

(58)

Therefore, the overall Grover operator G possesses the following eigen-relation:

ㅤ

G⁢|i⟩⁢|m⟩⁢|ω±⟩i⁢m=ei⁢(±2⁢θi⁢m)⁢|i⟩⁢|m⟩⁢|ω±⟩i⁢m.

ㅤ

(59)

Next, we apply phase estimation of the overall Grover operator G on the input state |Ψ1⟩. The resulting state |Ψ2⟩ can be written as

ㅤ

|Ψ2⟩=∑i∑m−i2⁢(ei⁢θi⁢m⁢|i⟩⁢|m⟩⁢|ω+⟩i⁢m⁢|2⁢θi⁢m⟩−ei⁢(−θi⁢m)⁢|i⟩⁢|m⟩⁢|ω−⟩i⁢m⁢|−2⁢θi⁢m⟩).

ㅤ

(60)

Note here in Eq. 60, |±2⁢θi⁢m⟩ denotes the eigenvalues ±2⁢θi⁢m being stored in the amplitude register with some finite precision.

Then we apply an oracle UO (implemented by arithmetic circuit) on the amplitude register and an extra ancilla register |0⟩𝖱𝖾𝖫𝖴, which acts as

ㅤ

UO⁢|0⟩𝖱𝖾𝖫𝖴⁢|±2⁢θi⁢m⟩=|ReLU⁡(𝒚i(m))⟩⁢|±2⁢θi⁢m⟩,

ㅤ

(61)

The state after the oracle can be written as

ㅤ

|Ψ3⟩=∑i∑m−i2⁢|ReLU⁡(𝒚i(m))⟩⁢(ei⁢θi⁢m⁢|i⟩⁢|m⟩⁢|ω+⟩i⁢m⁢|2⁢θi⁢m⟩−ei⁢(−θi⁢m)⁢|i⟩⁢|m⟩⁢|ω−⟩i⁢m⁢|−2⁢θi⁢m⟩).

ㅤ

(62)

Then we perform the uncomputation of Phase estimation, resulting in the state,

ㅤ	\|Ψ4⟩=∑i∑m−i2⁢\|ReLU⁡(𝒚i(m))⟩⁢(ei⁢θi⁢m⁢\|i⟩⁢\|m⟩⁢\|ω+⟩i⁢m⁢\|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t−ei⁢(−θi⁢m)⁢\|i⟩⁢\|m⟩⁢\|ω−⟩i⁢m⁢\|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t)	ㅤ	(63)
ㅤ	=∑i∑m\|ReLU⁡(𝒚i(m))⟩⁢\|i⟩⁢\|m⟩⁢\|ϕi⁢m⟩⁢\|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t	ㅤ	(64)

Refer to caption

Finally, we perform U† and the resulting state is

ㅤ

|Ψ5⟩=∑i∑m|ReLU⁡(𝒚i(m))⟩⁢|i⟩⁢|m⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩⁢|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t.

ㅤ

(65)

The above steps, as gathered in the grey box in Fig. 10, implement an oracle O𝖥𝖥𝖭 such that:

ㅤ

O𝖥𝖥𝖭:|i⟩⁢|m⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩⁢|0⟩𝖱𝖾𝖫𝖴→|i⟩⁢|m⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩⁢|ReLU⁡(𝒚i(m))⟩

ㅤ

(66)

Which produces the state

ㅤ

∑i∑m|i⟩⁢|m⟩⁢|𝒚′i(m)⟩⁢|0⟩k,h⁢|0⟩𝗈𝗍𝗁𝖾𝗋⁢|0⟩

ㅤ

(67)

where we denote 𝒚′i(m)=ReLU⁡(𝒚i(m)).

Next, the ”Conditional Rotation” (Theorem 3.5 in Ref. Landman (2021)) and uncomputation of O𝖥𝖥𝖭 are applied, obtaining

ㅤ

∑i∑m|i⟩⁢𝒚′i(m)⁢|m⟩=∑i|i⟩⁢∑m𝒚′i(m)⁢|m⟩=∑i|i⟩⁢|𝒚′i⟩

ㅤ

(68)

where |𝒚′i⟩:=∑m𝒚′i(m)⁢|m⟩ and we omitted the registers being in ”all-zero” state.

Finally, a trainable unitary U𝐖2 (a parameterised quantum circuit) implementing 𝐖2⊤ is applied

ㅤ

|Ψ𝑭⟩=∑i|i⟩⁢U𝐖2⁢|𝒚′i⟩=∑i|i⟩⁢|𝒇i⟩

ㅤ

(69)

where 𝒇i:=𝐖2⊤⁢𝒚′i=FFN⁡(𝒛i′)∈ℝr⁢H and we define 𝑭:=[𝒇1,…,𝒇n]∈ ℝr⁢H×n.

By the end of the quantum circuit in Fig. 10, we have obtained the final state from a Transformer block.

A tomography procedure (Theorem 4.3 from Ref.Landman (2021)) is performed to read out the amplitudes of the final state of a Transformer block. The results are then used as the input for the next Transformer block.

3.5 Generative Pre-training on Quantum Computer

Using the same notation as in the previous section, we denote the final state from the last Transformer block in GPT as:

ㅤ

|Ψ𝑭⟩=∑i|i⟩⁢|𝒇i⟩

ㅤ

(70)

where 𝒇i∈ℝr⁢H and 𝑭:=[𝒇1,…,𝒇n]∈ ℝr⁢H×n.

For language modeling, we then apply a linear layer 𝑾E∈ℝV×r⁢H to map the output back to the vocabulary space as 𝒇′i=𝑾E⁢𝒇i∈ℝV. 𝑾E can be implemented on a quantum circuit by applying a trainable unitary U𝑾E (a parameterised quantum circuit) on R⁢e⁢g⁢(k),R⁢e⁢g⁢(m) and some extra qubits (since V≫r⁢H) and we obtain the state

ㅤ

|Ψ𝑭′⟩=U𝑾E⁢(|Ψ𝑭⟩⊗|0⟩)=∑i|i⟩⁢U𝑾E⁢(|𝒇i⟩⊗|0⟩)=∑i|i⟩⁢|𝒇′i⟩

ㅤ

(71)

where 𝑭′:=[𝒇′1,…,𝒇′n]∈ ℝV×n.

For the tth batch in Generative Pre-training, we examine 𝒇′t+1 in the output, given the input [𝒙1,…,𝒙t]. The loss function for this batch is defined as the cross-entropy between softmax⁡(𝒇′t+1) and the one-hot encoding of the (t+1)th token in the training text, denoted by 𝒃t+1∈𝔹V. On the quantum circuit, the loss function can be correspondingly defined as the overlap between |𝒇′t+1⟩ and |𝒃t+1⟩12, which can be evaluated via swap test on |Ψ𝑭′⟩=∑i|i⟩⁢|𝒇′i⟩ and an additional state |Ψ𝒃t+1⟩=|t+1⟩⁢|𝒃t+1⟩. The cumulative loss is calculated across all batches, followed by the execution of certain optimization methods to adjust the model’s parameters.

4 Conclusion

In this paper, we have presented a comprehensive framework for translating key components of the GPT architecture—namely, the masked multi-head attention module, the feed-forward networks module, and the residual connection—along with the generative pre-training phase, into the quantum computing paradigm. This translation demonstrates the feasibility of implementing complex language models on quantum computers, marking an initial step toward harnessing the power of quantum computing to enhance the capabilities of LLMs. As we progress, it becomes imperative to conduct a detailed analysis of the quantum resources required for our quantum implementation of GPT, such as the number of qubits and circuit depths, and to perform a thorough comparison with classical GPT implementations.

In summary, the integration of quantum computing with LLMs, as demonstrated by our work, opens new avenues for research and development in the field of QML. By continuing to explore these possibilities, we move closer to realizing the full potential of quantum-enhanced artificial intelligence, setting the stage for future breakthroughs in computational efficiency and model capabilities.

References

Scholten et al. (2024) Travis L Scholten, Carl J Williams, Dustin Moody, Michele Mosca, William Hurley, William J Zeng, Matthias Troyer, Jay M Gambetta, et al., “Assessing the benefits and risks of quantum computers,” arXiv preprint arXiv:2401.16317 (2024).

Cerezo et al. (2022) Marco Cerezo, Guillaume Verdon, Hsin-Yuan Huang, Lukasz Cincio, and Patrick J Coles, “Challenges and opportunities in quantum machine learning,” Nature Computational Science 2, 567–576 (2022).

Liu et al. (2024) Junyu Liu, Minzhao Liu, Jin-Peng Liu, Ziyu Ye, Yunfei Wang, Yuri Alexeev, Jens Eisert, and Liang Jiang, “Towards provably efficient quantum algorithms for large-scale machine-learning models,” Nature Communications 15, 434 (2024).

Gao et al. (2023) Yeqi Gao, Zhao Song, Xin Yang, and Ruizhe Zhang, “Fast quantum algorithm for attention computation,” arXiv preprint arXiv:2307.08045 (2023).

Radford et al. (2018) Alec Radford, Karthik Narasimhan, Tim Salimans, Ilya Sutskever, et al., “Improving language understanding by generative pre-training,” (2018).

Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Lukasz Kaiser, and Illia Polosukhin, “Attention is all you need,” in Advances in neural information processing systems, Vol. 30 (2017).

Liu et al. (2018) Peter J Liu, Mohammad Saleh, Etienne Pot, Ben Goodrich, Ryan Sepassi, Lukasz Kaiser, and Noam Shazeer, “Generating wikipedia by summarizing long sequences,” arXiv preprint arXiv:1801.10198 (2018).

Medsker and Jain (1999) Larry Medsker and Lakhmi C Jain, Recurrent neural networks: design and applications (CRC press, 1999).

Ghojogh and Ghodsi (2020) Benyamin Ghojogh and Ali Ghodsi, “Attention mechanism, transformers, bert, and gpt: tutorial and survey,” OSF Preprints (2020).

Jurafsky and Martin (2021) Daniel Jurafsky and James H. Martin, Speech and Language Processing, 3rd ed. (Pearson, 2021).

Brown et al. (1992) Peter F Brown, Vincent J Della Pietra, Stephen A Della Pietra, and Robert L Mercer, “Class-based n-gram models of natural language,” Computational linguistics 18, 467–479 (1992).

Hochreiter and Schmidhuber (1997) Sepp Hochreiter and Jürgen Schmidhuber, “Long short-term memory,” Neural Computation 9, 1735–1780 (1997).

Mikolov et al. (2013) Tomas Mikolov, Kai Chen, Greg Corrado, and Jeff Dean, “Efficient estimation of word representations in vector space,” arXiv preprint arXiv:1301.3781 (2013).

Pennington et al. (2014) Jeffrey Pennington, Richard Socher, and Christopher D Manning, “Glove: Global vectors for word representation,” in Proceedings of the 2014 Conference on Empirical Methods in Natural Language Processing (EMNLP) (2014) pp. 1532–1543.

Goldberg and Levy (2014) Yoav Goldberg and Omer Levy, “word2vec explained: deriving mikolov et al.’s negative-sampling word-embedding method,” arXiv preprint arXiv:1402.3722 (2014).

Mikolov et al. (2015) Tomas Mikolov, Quoc V Le, and Ilya Sutskever, “Computing numeric representations of words in a high-dimensional space,” in Machine Learning and Knowledge Discovery in Databases (Springer, 2015) pp. 522–536.

Yuan and Zhang (2023) Pei Yuan and Shengyu Zhang, “Optimal (controlled) quantum state preparation and improved unitary synthesis by quantum circuits with any number of ancillary qubits,” Quantum 7, 956 (2023).

Lu et al. (2021) Jiachen Lu, Jinghan Yao, Junge Zhang, Xiatian Zhu, Hang Xu, Weiguo Gao, Chunjing Xu, Tao Xiang, and Li Zhang, “Soft: Softmax-free transformer with linear complexity,” Advances in Neural Information Processing Systems 34, 21297–21309 (2021).

Qin et al. (2022) Zhen Qin, Weixuan Sun, Hui Deng, Dongxu Li, Yunshen Wei, Baohong Lv, Junjie Yan, Lingpeng Kong, and Yiran Zhong, “cosformer: Rethinking softmax in attention,” arXiv preprint arXiv:2202.08791 (2022).

Nguyen et al. (2022) Quynh T Nguyen, Bobak T Kiani, and Seth Lloyd, “Block-encoding dense and full-rank kernels using hierarchical matrices: applications in quantum numerical linear algebra,” Quantum 6, 876 (2022).

Velickovic et al. (2017) Petar Velickovic, Guillem Cucurull, Arantxa Casanova, Adriana Romero, Pietro Lio, and Yoshua Bengio, “Graph attention networks,” in Proc. of ICLR (2017).

He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun, “Deep residual learning for image recognition,” in Proc. of CVPR (2016) pp. 770–778.

Allcock et al. (2020) Jonathan Allcock, Chang-Yu Hsieh, Iordanis Kerenidis, and Shengyu Zhang, “Quantum algorithms for feedforward neural networks,” ACM Transactions on Quantum Computing 1 (2020).

Brassard et al. (2002) Gilles Brassard, Peter Hoyer, Michele Mosca, and Alain Tapp, “Quantum amplitude amplification and estimation,” Contemporary Mathematics 305, 53–74 (2002).

Landman (2021) Jonas Landman, “Quantum algorithms for unsupervised machine learning and neural networks,” arXiv preprint arXiv:2111.03598 (2021).

Liao et al. (2021) Yidong Liao, Min-Hsiu Hsieh, and Chris Ferrie, “Quantum optimization for training quantum neural networks,” arXiv preprint arXiv:2103.17047 (2021).

Sünderhauf et al. (2024) Christoph Sünderhauf, Earl Campbell, and Joan Camps, “Block-encoding structured matrices for data input in quantum computing,” Quantum 8, 1226 (2024).

Childs and Wiebe (2012) Andrew M. Childs and Nathan Wiebe, “Hamiltonian simulation using linear combinations of unitary operations,” arXiv:1202.5822 (2012).

Lin (2022) Lin Lin, “Lecture notes on quantum algorithms for scientific computation,” arXiv preprint arXiv:2201.08309 (2022).

Larocca et al. (2023) Martin Larocca, Nathan Ju, Diego García-Martín, Patrick J. Coles, and M. Cerezo, “Theory of overparametrization in quantum neural networks,” Nature Computational Science 3, 542––551 (2023).

Kandala et al. (2017) Abhinav Kandala, Antonio Mezzacapo, Kristan Temme, Maika Takita, Markus Brink, Jerry M. Chow, and Jay M. Gambetta, “Hardware-efficient variational quantum eigensolver for small molecules and quantum magnets,” Nature 549, 242–246 (2017).

Hadfield et al. (2019) Stuart Hadfield, Zhihui Wang, Bryan O’Gorman, Eleanor G Rieffel, Davide Venturelli, and Rupak Biswas, “From the quantum approximate optimization algorithm to a quantum alternating operator ansatz,” Algorithms 12, 34 (2019).

Choquette et al. (2021) Alexandre Choquette, Agustin Di Paolo, Panagiotis Kl Barkoutsos, David Sénéchal, Ivano Tavernelli, and Alexandre Blais, “Quantum-optimal-control-inspired ansatz for variational quantum algorithms,” Physical Review Research 3, 023092 (2021).

Goodfellow et al. (2016) Ian Goodfellow, Yoshua Bengio, and Aaron Courville, Deep learning (MIT press, 2016).

Appendix A Quantum Attention Oracle

In this section, we introduce the construction of the quantum attention oracle O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇, as mentioned in Section 3.2.1. The quantum attention oracle O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇 is designed to coherently evaluate and store the attention score a⁢(𝕩i,𝕩j) for each pair of input vectors 𝕩i and 𝕩j. It acts as follows:

ㅤ

O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇⁢|i⟩⁢|j⟩⁢|0⟩→|i⟩⁢|j⟩⁢|a⁢(𝕩i,𝕩j)⟩.

ㅤ

(72)

The construction of O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇 consists of the following two steps:

A.1 Evaluating Attention score in superposition

The attention score a⁢(𝕩i,𝕩j) can take one of the standard forms in the classical literature Ghojogh and Ghodsi (2020) — the inner product of the linearly transformed input vectors:

ㅤ

a⁢(𝕩i,𝕩j)=𝕩iT⁢WKT⁢WQ⁢𝕩j,

ㅤ

(73)

where WK,WQ are trainable linear transformations.

In terms of Dirac notation, this can be written as:

ㅤ

a⁢(𝕩i,𝕩j)=⟨𝕩i|UK†⁢UQ|𝕩j⟩

ㅤ

(74)

in which UK,UQ are trainable unitaries, |𝕩i⟩:=∑k=1d𝕩i(k)⁢|k⟩ is the amplitude encoding of the vector 𝕩i whose k-th elements are denoted as 𝕩i(k). Note here and throughout the paper, we omit the normalization factors.

This attention score can be evaluated on a quantum circuit by parallel swap test Liao et al. (2021) as depicted in Fig. 11 which we will discuss in detail below.

Refer to caption

We denote the unitary for the parallel swap test circuit, as circled by the pink box on the left side of Fig. 11, as U. The input to U, |Ψ0⟩, can be written as (note here and throughout the paper, we omit the normalization factors):

ㅤ

|Ψ0⟩=|0⟩⊗(∑i|i⟩)⊗|0⟩𝙺n⊗(∑j|j⟩)⊗|0⟩𝚀n

ㅤ

(75)

where |0⟩𝙺n,|0⟩𝚀n are the initial states of the two registers on which the input vectors will be loaded. The input encoding via Controlled Quantum State PreparationYuan and Zhang (2023)(mentioned in Section 3.2.1), depicted as the blue boxes in Fig.11, can be written as ∑i|i⟩⁢⟨i|⊗U𝕩i where U𝕩i act as U𝕩i⁢|0⟩=|𝕩i⟩.

Applying this input encoding results in the following state:

ㅤ

|Ψ1⟩=|0⟩⊗(∑i|i⟩⊗|𝕩i⟩n)⊗(∑j|j⟩⊗|𝕩j⟩n)

ㅤ

(76)

Then, UK,UQ implemented by parametrized quantum circuits are applied on the two registers hosting the input vectors, yielding the following state:

ㅤ

|Ψ2⟩=|0⟩⊗(∑i|i⟩⊗UK⁢|𝐱i⟩n)⊗(∑j|j⟩⊗UQ⁢|𝕩j⟩n)

ㅤ

(77)

ㅤ

U≔[H⊗I⊗I⊗I⊗I]⋅[|0⟩⟨0|⊗(∑i∑j|i⟩⟨i|⊗𝒦i⊗|j⟩⟨j|⊗𝒬j)+|1⟩⟨1|⊗(∑i∑j|i⟩⟨i|⊗𝒬j⊗|j⟩⟨j|⊗𝒦i)]⋅[H⊗I⊗I⊗I⊗I].

ㅤ

(78)

Reorganizing the terms in Eqn 78 we have

ㅤ

U=∑i∑j|i⟩⟨i|⊗|j⟩⟨j|⊗Ui⁢j,

ㅤ

(79)

where

ㅤ

Ui⁢j≔[H⊗I⊗I]⋅[|0⟩⁢⟨0|⊗𝒦i⊗𝒬j+|1⟩⁢⟨1|⊗𝒬j⊗𝒦i]⋅[H⊗I⊗I],

ㅤ

(80)

Define |ϕi⁢j⟩≔Ui⁢j⁢|0⟩⁢|0⟩𝙺n⁢|0⟩𝚀n and we have:

ㅤ

|ϕi⁢j⟩=12⁢(|+⟩⁢|ki⟩⁢|qj⟩+|−⟩⁢|qj⟩⁢|ki⟩).

ㅤ

(81)

Expanding and rearranging the terms in Eq. 81 we have

ㅤ

|ϕi⁢j⟩=12(|0⟩⊗(|ki⟩|qj⟩+|qj⟩|ki⟩)+|1⟩⊗(|ki⟩|qj⟩−|qj⟩|ki⟩).

ㅤ

(82)

Denote |ui⁢j⟩ and |vi⁢j⟩ as the normalized states of |ki⟩⁢|qj⟩+|qj⟩⁢|ki⟩ and |ki⟩⁢|qj⟩−|qj⟩⁢|ki⟩ respectively. Then there is a real number θi⁢j∈[π/4,π/2] such that

ㅤ

|ϕi⁢j⟩=sin⁡θi⁢j⁢|0⟩⁢|ui⁢j⟩+cos⁡θi⁢j⁢|1⟩⁢|vi⁢j⟩.

ㅤ

(83)

θi⁢j satisfies cos⁡θi⁢j=1−|⟨ki|qj⟩|2/2, sin⁡θi⁢j=1+|⟨ki|qj⟩|2/2.

The final output state from U, |Ψ3⟩=U⁢|Ψ0⟩, can then be written as

ㅤ

|Ψ3⟩=∑i∑j|i⟩|j⟩(sinθi⁢j|ui⁢j⟩|0⟩+cosθi⁢j|vi⁢j⟩|1⟩)⏟∣ϕi⁢j⟩=∑i∑j|i⟩|j⟩|ϕi⁢j⟩

ㅤ

(84)

Note that ⟨ki|qj⟩=⟨𝕩i|UK†⁢UQ|𝕩j⟩=a⁢(𝕩i,𝕩j) being the attention scores are encoded in the amplitudes of the output state |Ψ3⟩ of swap test as:

ㅤ

|⟨ki|qj⟩|2=−cos⁡2⁢θi⁢j.

ㅤ

(85)

A.2 Storing Attention score

The second step is to use amplitude estimation Brassard et al. (2002) to extract and store the attention scores into an additional register which we call the “amplitude register”.

After step 1, we introduce an extra register |0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t and the output state |Ψ3⟩ (using the same notation) becomes

ㅤ

|Ψ3⟩=∑i∑j|i⟩⁢|j⟩⁢|ϕi⁢j⟩⁢|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t,

ㅤ

(86)

where |ϕi⁢j⟩ can be decomposed as

ㅤ

|ϕi⁢j⟩=−i2⁢(ei⁢θi⁢j⁢|ω+⟩i⁢j−ei⁢(−θi⁢j)⁢|ω−⟩i⁢j).

ㅤ

(87)

Hence, we have

ㅤ

|Ψ3⟩=∑i∑j−i2⁢(ei⁢θi⁢j⁢|i⟩⁢|j⟩⁢|ω+⟩i⁢j−ei⁢(−θi⁢j)⁢|i⟩⁢|j⟩⁢|ω−⟩i⁢j)⁢|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t.

ㅤ

(88)

The overall Grover operator G is defined as

ㅤ

G≔U⁢C2⁢U†⁢C1,

ㅤ

(89)

where C1 is the Z gate on the swap ancilla qubit, and C2=I−2⁢|0⟩⁢⟨0| is the “flip zero state” on registers other than the two registers hosting indices i,j (represented as S0 in Fig.12). It can be shown that G can be expressed as

ㅤ

G=∑i∑j|i⟩|j⟩⟨j|⟨i|⊗Gi⁢j,

ㅤ

(90)

where Gi⁢j is defined as

ㅤ

Gi⁢j=(I−2|ϕi⁢j⟩⟨ϕi⁢j|))C1

ㅤ

(91)

It is easy to check that |w±⟩i⁢j are the eigenstates of Gi⁢j, that is,

ㅤ

Gi⁢j⁢|w±⟩i⁢j=e±𝒊⁢2⁢θi⁢j⁢|w±⟩i⁢j.

ㅤ

(92)

The overall Grover operator G possesses the following eigen-relation:

ㅤ

G⁢|i⟩⁢|j⟩⁢|ω±⟩i⁢j=ei⁢(±2⁢θi⁢j)⁢|i⟩⁢|j⟩⁢|ω±⟩i⁢j.

ㅤ

(93)

Next, we apply phase estimation of the overall Grover operator G on the input state |Ψ3⟩. The resulting state |Ψ4⟩ can be written as

ㅤ

|Ψ4⟩=∑i∑j−i2⁢(ei⁢θi⁢j⁢|i⟩⁢|j⟩⁢|ω+⟩i⁢j⁢|2⁢θi⁢j⟩−ei⁢(−θi⁢j)⁢|i⟩⁢|j⟩⁢|ω−⟩i⁢j⁢|−2⁢θi⁢j⟩).

ㅤ

(94)

Note here in Eq. 94, |±2⁢θi⁢j⟩ denotes the eigenvalues ±2⁢θi⁢j being stored in the amplitude register with some finite precision.

Next, we apply an oracle UO (implemented by arithmetic circuit) on the amplitude register and an extra ancilla register, which acts as

ㅤ

UO⁢|0⟩⁢|±2⁢θi⁢j⟩=|a⁢(𝕩i,𝕩j)⟩⁢|±2⁢θi⁢j⟩,

ㅤ

(95)

The state after the oracle can be written as

ㅤ

|Ψ5⟩=∑i∑j−i2⁢|a⁢(𝕩i,𝕩j)⟩⁢(ei⁢θi⁢j⁢|i⟩⁢|j⟩⁢|ω+⟩i⁢j⁢|2⁢θi⁢j⟩−ei⁢(−θi⁢j)⁢|i⟩⁢|j⟩⁢|ω−⟩i⁢j⁢|−2⁢θi⁢j⟩).

ㅤ

(96)

Then we perform the uncomputation of Phase estimation, the resulting state is

ㅤ	\|Ψ6⟩=∑i∑j−i2⁢\|a⁢(𝕩i,𝕩j)⟩⁢(ei⁢θi⁢j⁢\|i⟩⁢\|j⟩⁢\|ω+⟩i⁢j⁢\|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t−ei⁢(−θi⁢j)⁢\|i⟩⁢\|j⟩⁢\|ω−⟩i⁢j⁢\|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t)	ㅤ	(97)
ㅤ	=∑i∑j\|a⁢(𝕩i,𝕩j)⟩⁢\|i⟩⁢\|j⟩⁢\|ϕi⁢j⟩⁢\|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t	ㅤ	(98)

Finally, we perform the uncomputation of the swap test and the resulting state is

ㅤ

|Ψ7⟩=∑i∑j|a⁢(𝕩i,𝕩j)⟩⁢|i⟩⁢|j⟩⁢|0⟩⁢|0⟩𝘢𝘮𝘱𝘭𝘪𝘵𝘶𝘥𝘦t.

ㅤ

(99)

The above steps, as illustrated in Fig. 12, implemented the quantum attention oracle O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇 such that:

ㅤ

O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇⁢|i⟩⁢|j⟩⁢|0⟩→|i⟩⁢|j⟩⁢|a⁢(𝕩i,𝕩j)⟩

ㅤ

(100)

Figure 12: Quantum attention oracle O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇subscript𝑂𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇O_{\textsf{attention}}italic_O start_POSTSUBSCRIPT attention end_POSTSUBSCRIPT The quantum attention oracle aims to coherently evaluate and store attention score a⁢(𝕩i,𝕩j)𝑎subscript𝕩𝑖subscript𝕩𝑗a(\mathbb{x}_{i},\mathbb{x}_{j})italic_a ( blackboard_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT , blackboard_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ) for each pair of the input vectors, it acts as O𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇⁢|i⟩⁢|j⟩⁢|0⟩→|i⟩⁢|j⟩⁢|a⁢(𝕩i,𝕩j)⟩→subscript𝑂𝖺𝗍𝗍𝖾𝗇𝗍𝗂𝗈𝗇ket𝑖ket𝑗ket0ket𝑖ket𝑗ket𝑎subscript𝕩𝑖subscript𝕩𝑗O_{\textsf{attention}}\left|i\right\rangle\left|j\right\rangle\left|0\right% \rangle\to\left|i\right\rangle\left|j\right\rangle\left|a(\mathbb{x}_{i},% \mathbb{x}_{j})\right\rangleitalic_O start_POSTSUBSCRIPT attention end_POSTSUBSCRIPT | italic_i ⟩ | italic_j ⟩ | 0 ⟩ → | italic_i ⟩ | italic_j ⟩ | italic_a ( blackboard_x start_POSTSUBSCRIPT italic_i end_POSTSUBSCRIPT , blackboard_x start_POSTSUBSCRIPT italic_j end_POSTSUBSCRIPT ) ⟩. The construction of the quantum attention oracle, depicted in this figure, is detailed in the appendix subsections A.1 and A.2.

Appendix B Positional encoding via quantum circuit

The positional encoding mentioned in Section 2.1 can be described as followsGhojogh and Ghodsi (2020): Corresponding to the i-th vector in the sequence 𝒙i∈ℝd, define the position vector 𝒑i∈ℝd as:

ㅤ

{𝒑i(2⁢j+1):=cos⁡(i100002⁢jd)𝒑i(2⁢j):=sin⁡(i100002⁢jd)

ㅤ

(101)

for all j∈{0,1,…,⌊d/2⌋}, where 𝒑i(2⁢j+1) and 𝒑i(2⁢j) denote the odd and even elements of 𝒑i, respectively. For encoding of positional information into data, the position vectors are added directly to the input vectors:

ㅤ

𝒙′i=𝒙i+𝒑i,

ㅤ

(102)

where 𝒙′i is the appended input vectors that contain positional information, and we define 𝑿′:=[𝒙′1,…,𝒙n′]∈ℝd×n. as the matrix by stacking 𝒙′i.

Our quantum algorithm for positional encoding aims to create the quantum state

ㅤ

|ψ𝑿′⟩:=∑i=1n|i⟩⁢|𝒙′i⟩,

ㅤ

(103)

where |𝒙′i⟩:=∑k=1d𝒙′i(k)⁢|k⟩ is the amplitude encoding of the vector 𝒙′i whose k-th elements are denoted as 𝒙′i(k). Similarly, we define |𝒑i⟩:=∑k=1d𝒑i(k)⁢|k⟩ which is the amplitude encoding of the vector 𝒑i whose k-th elements are denoted as 𝒑i(k) and

ㅤ

|ψ𝑷⟩:=∑i=1n|i⟩⁢|𝒑i⟩

ㅤ

(104)

From the above definitions of |𝒙′i⟩,|𝒑i⟩ and Eqn. 2102103104 we have

ㅤ

|ψ𝑿′⟩=|ψ𝑿⟩+|ψ𝑷⟩=∑i=1n|i⟩⁢|𝒙i⟩+∑i=1n|i⟩⁢|𝒑i⟩

ㅤ

(105)

Note that

ㅤ

|𝒑i⟩=∑k=1d𝒑i(k)⁢|k⟩=∑j(𝒑i(2⁢j)⁢|2⁢j⟩+𝒑i(2⁢j+1)⁢|2⁢j+1⟩)

ㅤ

(106)

Denote the unitary that prepares |ψ𝑷⟩ from ∑i=1n|i⟩⁢|0⟩ as U𝑷, then |ψ𝑿′⟩ can be achieved by applying LCU to U𝑿,U𝑷. As the construction of U𝑿 is given by the CQSP mentioned in Section 3.1, we can focus on the construction of U𝑷. Next, we present the construction of U𝑷 as depicted in Fig.13.

Refer to caption

Build upon the two registers R⁢e⁢g⁢(i) and R⁢e⁢g⁢(k) hosting the index i and k respectively (illustrated in Fig. 6), in Fig. 13, we set up a register R⁢e⁢g⁢(j) hosting the index j below R⁢e⁢g⁢(i) and an ancillary qubit above R⁢e⁢g⁢(i). For reasons that will be clear soon, we combine R⁢e⁢g⁢(j) and the ancillary qubit as a single register which coincides with R⁢e⁢g⁢(k). The blue boxes that group the series of controlled RY gates implement the following unitaries:

ㅤ

Pj=∑i|i⟩⁢⟨i|⊗Ry⁢(−2⁢i⁢wj)

ㅤ

(107)

each of which is controlled by the qubits in R⁢e⁢g⁢(j), and the entire controlled sequences grouped in the transparent box implement the unitary

ㅤ

Uc=∑j|j⟩⁢⟨j|⊗Pj=∑j|j⟩⁢⟨j|⊗∑i|i⟩⁢⟨i|⊗Ry⁢(−2⁢i⁢wj)

ㅤ

(108)

The Hadamard gates and X gate before Uc transform the input state to the state ∑j|j⟩⊗∑i|i⟩⊗|1⟩, after Uc, it becomes

ㅤ

Uc⁢(∑j|j⟩⊗∑i|i⟩⊗|1⟩)=∑j|j⟩⊗∑i|i⟩⊗Ry⁢(−2⁢i⁢wj)⁢|1⟩

ㅤ

(109)

By placing R⁢e⁢g⁢(j) and the ancillary qubit next to each other we can rewrite the above state as:

ㅤ	∑i\|i⟩⊗∑j\|j⟩⊗Ry⁢(−2⁢i⁢wj)⁢\|1⟩	ㅤ	(110)
ㅤ	=∑i\|i⟩⊗∑j\|j⟩⊗(sin⁡(i⁢wj)⁢\|0⟩+cos⁡(i⁢wj)⁢\|1⟩).	ㅤ	(111)

Combining R⁢e⁢g⁢(j) and the ancillary qubit as a single register that coincides with R⁢e⁢g⁢(k), the computational basis transform as |j⟩⁢|0⟩→|2⁢j⟩,|j⟩⁢|1⟩→|2⁢j+1⟩ and we can write the output state from the circuit in Fig.13 as:

ㅤ

|output⟩=∑i|i⟩⊗∑j(sin⁡(i⁢wj)⁢|2⁢j⟩+cos⁡(i⁢wj)⁢|2⁢j+1⟩)

ㅤ

(112)

set w=1100001d, and from Eqn. 101104106112 we have

ㅤ

|output⟩=|ψ𝑷⟩

ㅤ

(113)

That is, the circuit in Fig.13 implements U𝑷.

Appendix C Masked-Attention

This section presents the masking operation in attention and its quantum implementation.

The masked attention is defined as:Ghojogh and Ghodsi (2020)

ㅤ	ℝr×n∋𝒁m	:=maskedAttention⁡(𝑸,𝑲,𝑽)	ㅤ
ㅤ	ㅤ	=𝑽⁢softmax⁡(1p⁢(𝑸⊤⁢𝑲+𝑴)),	ㅤ

where the mask matrix 𝑴∈ℝn×n is:

ㅤ

𝑴i⁢j:={0 if ⁢j⩽i−∞ if ⁢j>i

ㅤ

For positions j⩽i in a sequence (representing current or previous words), the mask doesn’t alter the softmax output, this allows these positions to contribute to the softmax computation. In contrast, for positions j>i (corresponding to future words in the sequence), the nature of softmax function indicates that the mask effectively nullifies their contribution as e−∞ is 0. This selective masking ensures that the model’s attention is appropriately focused on the relevant parts of the sequence: considering past and present words while ignoring future words.

Denoting 𝑨0𝖬𝖺𝗌𝗄≡softmax⁡(1p⁢(𝑸⊤⁢𝑲+𝑴)), we have its elements as

ㅤ

𝑨0𝖬𝖺𝗌𝗄i⁢j:={𝑨0i⁢j if ⁢j⩽i0 if ⁢j>i

ㅤ

where 𝑨0i⁢j is the elements of 𝑨0≡softmax⁡(1p⁢𝑸⊤⁢𝑲).

In the quantum case, we aim to implement an alternative version of 𝑨0𝖬𝖺𝗌𝗄 denoted as 𝑨𝖬𝖺𝗌𝗄 whose elements are defined as

ㅤ

𝑨𝖬𝖺𝗌𝗄i⁢j:={𝑨i⁢j if ⁢j⩽i0 if ⁢j>i

ㅤ

where 𝑨i⁢j is the elements of 𝑨≡𝑸⊤⁢𝑲.

For masked-attention, we aim to design a quantum circuit implementing the following computation:

ㅤ

𝒁′m=𝑾V⊤⁢𝑿⁢𝑨𝖬𝖺𝗌𝗄,

ㅤ

(114)

This can be done in a similar way as in the case of self-attention where we implemented Eqn.12, the only difference is that we now need the block-encoding of 𝑨𝖬𝖺𝗌𝗄⊤ (instead of 𝑨⊤) whose elements are

ㅤ

Λi⁢j𝖬𝖺𝗌𝗄:=𝑨𝖬𝖺𝗌𝗄i⁢j⊤:={0 if ⁢j<i𝑨j⁢i if ⁢j⩾i

ㅤ

Similar to the case of self-attention, let Λ^𝖬𝖺𝗌𝗄⩾maxi,j⁡|Λi⁢j𝖬𝖺𝗌𝗄| and Λ~i⁢j𝖬𝖺𝗌𝗄 is defined to be the (exact) b-qubit description of Λi⁢j𝖬𝖺𝗌𝗄/Λ^𝖬𝖺𝗌𝗄. The block-encoding of 𝑨𝖬𝖺𝗌𝗄⊤ can be constructed using lemma 3.2 from Ref.Nguyen et al. (2022), given the following oracle

ㅤ

O𝑨𝖬𝖺𝗌𝗄⊤:|i⟩⁢|j⟩⁢|0⟩⊗b→|i⟩⁢|j⟩⁢|Λ~i⁢j𝖬𝖺𝗌𝗄⟩,

ㅤ

(115)

where 0⩽i,j<n.

This oracle O𝑨𝖬𝖺𝗌𝗄⊤ can be constructed by conditionally applying O𝑨⊤: on the registers hosting |i⟩⁢|j⟩, set up a circuit comparing the values of i,j with the result stored in an extra ancillary qubit (using Claim 3.1 in Ref.Landman (2021)). Then using this ancillary qubit as control qubit, apply controlled O𝑨⊤ if j⩾i.

Appendix D Block-encoding

Block encoding is a powerful modern quantum algorithmic technique that is employed in a variety of quantum algorithms for solving linear algebra problems on a quantum computerSünderhauf et al. (2024). A unitary U is a block encoding of a not-necessarily-unitary square matrix A (A is scaled to satisfy ‖A‖2⩽1Sünderhauf et al. (2024)) if A is encoded in the top-left block of the unitary U as:

ㅤ

U=[A.⋅⋅],

ㅤ

where the ⋅ symbol stands for a matrix block. Equivalently, we can write

ㅤ

A=(⟨0|⊗a⊗I)⁢U⁢(|0⟩⊗a⊗I)

ㅤ

(116)

where a is the number of ancilla qubits used for the block encoding of A. U can be considered as a probabilistic implementation of A: by applying the unitary U to an input state |0⟩⊗a⁢|b⟩, measuring the first a-qubit register and post-selecting on the outcome |0⟩⊗a, we obtain a state that is proportional to A⁢|b⟩ in the second register. This can be illustrated in Fig.14.

Figure 14: Block-encoding U, the Block-encoding of a matrix A, can be considered as a probabilistic implementation of A: applying the unitary U to a given input state |0 ⟩ ⊗ a ⁢ |b ⟩, measuring the first a-qubit register and post-selecting on the outcome |0 ⟩ ⊗ a, we get state proportional to A⁢ |b ⟩ in the second register.

The circuit implementation of Block-encoding in general can be constructed using the Linear Combination of Unitaries(LCU)Childs and Wiebe (2012) technique.Lin (2022)

Appendix E Parametrized quantum circuit for implementing trainable linear layer

Classical neural networks are fundamentally built on the structure of multilayer perceptrons which involve layers of trainable linear transformations and element-wise nonlinear transformations (activation functions such as ReLU, sigmoid, or tanh). On the other hand, Quantum Neural Networks (QNNs), which are often defined as parametrized quantum circuits with a predefined circuit ansatz, do not naturally exhibit this kind of structure. In QML literature, a QNN, denoted as U⁢(𝜽), often has a structure of layers L of the form Larocca et al. (2023)

ㅤ

U⁢(𝜽)=∏l=1LUl⁢(𝜽l),Ul⁢(𝜽l)=∏k=1Ke−i⁢θl⁢k⁢Hk,

ㅤ

(117)

where the index l represents the layer, and the index k covers the Hermitian operators Hk that generates the unitaries in the circuit ansatz, 𝜽l=(θl⁢1,…⁢θl⁢K) represents the parameters in a single layer, and 𝜽={𝜽1,…,𝜽L} represents the collection of adjustable parameters in the QNN. Examples of circuit ansatz represented by Eq. 117 include: the hardware-efficient ansatz Kandala et al. (2017), quantum alternating operator ansatz Hadfield et al. (2019), and quantum optimal control Ansatz Choquette et al. (2021), among others.

In machine learning, a linear layer Goodfellow et al. (2016) is a fundamental component of neural networks architectures that maps input vectors to output vectors through affine transformation: Given an input vector 𝐱∈ℝn, the linear layer transforms it to an output vector 𝐲∈ℝm using a weight matrix W∈ℝm×n and an optional bias vector 𝐛∈ℝm as 𝐲=W⁢𝐱+𝐛, and W, b contain the trainable parameters.

The input vector 𝐱 can be encoded in the amplitudes of a s-qubit quantum state (n=2s) |ψx⟩ as |ψx⟩=∑i=1nxi⁢|i⟩ where xi is the i-th element of 𝐱(after normalization), and |i⟩ is the i-th computational basis state. Applying a parameterized quantum circuit U⁢(𝜽)∈ℂn×n on |ψx⟩ be interpreted as a special type of linear layer (represented as a square matrix) on 𝐱. In this paper, we utilize parameterized quantum circuits as in Eq. 117 for implementing such linear layers. Note that in case where the weight matrix W∈ℝm×n is rectangular (m≠n), by default we adjust the dimension of the output vector to be the same as the input vector in our quantum architecture, without specifying the adjustment in the prior description of the classical architecture.

It should be emphasized that the trainable circuit parameters 𝜽 are not equivalent to the weights in the weight matrix, but rather are parameterized by them, as in W⁢(𝜽). Ref Larocca et al. (2023) contains a discussion of the parametrization.